Bayesian Optimization

만약 우리에게 모델이 있는데,

black-box function이라 예측은 잘 되는데 그 속을 들여다 볼 수 없다.

즉, f(x)가 closed-form으로 표현되지 않는다.

또 non-linear + non-convex 해서 gradient도 찾을 수 없다.

심지어 query를 입력으로 주고 evaluate 할 때 엄청난 시간/비용이 든다.

그래서 하이퍼파라미터를 튜닝하기 위해 여러번 시행착오를 겪을 수도 없다.

이렇게 우울한 모델이 있다면 어떻게 optimal model을 찾을 수 있을까?

가장 단순한 방법은 parameter를 grid로 나눠서 모든 모델을 만들어본다. (Grid Search)
하지만 생각만 해도 시간이 너무 많이 걸릴 것 같다.

그럼 grid를 모두 찾는게 아니고 random하게 parameter를 찍어볼 수 있다. (Random Search)
조금 빨리 찾을 가능성은 생기지만 역시나 효율적이진 않다.

이 때 효과적으로 하이퍼파라미터를 찾을 수 있는 훌륭한 방법으로 Bayesian Optimization를 사용할 수 있다.

Bayesian Optimization(이하 BO)는 어떤 함수가 최대/최소값을 갖게 하는 지점 x*를 찾는 일종의 Optimize 알고리즘이다.
(AutoML은 BO를 적용할 수 있는 한 분야일 뿐, AutoML을 위한 알고리즘이 아니다.)

대표적인 활용 사례는 아래와 같다.

1. Hyperparameter optimization : loss를 최소화 하는 모델의 하이퍼파라미터를 찾는 분야
※ 이걸 비즈니스로 하는 회사도 있다. (ex. SIGOPT)

2. Automated machine learning : 하이퍼파라미터를 포함해서 모델까지 찾는 분야

Auto ML은 현재 상당히 Hot 한 분야로 많은 기업에서 서비스를 제공하고 있다.

- Google : Cloud AutoML

- Facebook : AI that build AI

- Microsoft : in Azure Machine Learning

- Amazon : AutoGluon
("ML의 민주화!" 를 슬로건으로 걸만큼 굉장히 사용이 쉽다.)

※ AutoML ⊃ Hyperparameter Optimization ⊃ NAS

※ Meta Learning : Learning how to learn (학습을 어떻게 하는지 배우는 분야)

3. Clinical drug trial in healthcare : 신약 제조를 위해 최적을 조합을 찾는 분야

4. Active user modeling : AI 비서와 같이 어떤 답변을 해야할지 결정하는 분야

그럼 이제부터 BO가 얼마나 효과적으로 optimization 하는지 그 원리를 알아보도록 하자.

Bayesian Optimization

Bayesian Optimization은 말 그대로 Optimization을 Bayesian스럽게 한단 뜻이다.

즉, Bayes rule에 의해 사전지식(prior)을 반영하면서 하이퍼파라미터를 찾는다.

그 정의를 Model Optimization에 적용시키면 위와 같다.

즉, Bayesian Optimization는 현재까지 얻은 모델(prior)과 추가적인 실험 정보(likelihood)를 통해 데이터가 주어졌을 때의 모델(posterior)을 추정해 나가는 방식을 가진다.

자세히 들어가기 전에 일단 맛보기로 대략적인 BO의 원리를 살펴보자.

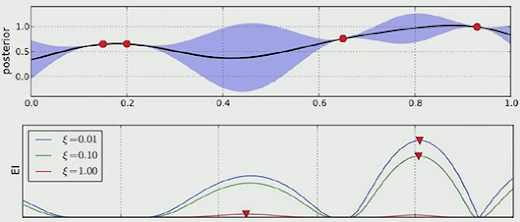
우리가 알 수 없는 미지의 함수 f (점선) 의 최대지점을 찾아보자.

우리는 함수는 모르지만 관측치는 알 수 있어서 2개의 점을 임의로 찍어서 GP regression을 수행하면,

위 그림과 같이 posterior mean function(bold line)과 posterior covariance(파란 음영)을 구할 수 있다.

이 때 mean과 covariance 값이 유독 큰 위치를 찾을 수 있다. (▼ acquisition max)

그럼 그 위치에 있는 관측값을 추가하여 다시 GP regression을 수행한다.

posterior mean과 covariance를 참고해 다음 관측지점을 또 찾는다. (▼)

다음 관측지점을 추가할 수록 추정 함수의 분산은 점점 작아지고 새로운 관측치는 점점 global maxima로 향해 가는 것을 볼 수 있다.

즉, 전체 관측치를 살펴볼 필요 없이 적은 횟수로 global maxima를 찾을 수 있다.

이것이 바로 Bayesian Optimization의 naive한 원리다.

(사실상 이 그림만 이해한다면 User로써 Bayesian Optimizer 원리는 다 이해한거다.)

위 예제를 소개하면서 중요한 함수를 2개 발견했을 것이다.

Surrogate function
: GP regression과 같이 관측치로 부터 f(·)를 예측하는 확률 모델이다.

Acquisition function
: 다음 관측치를 선택하기 위한 함수다. 위 예제에서 녹색 그래프로 표현됐다.

즉, posterior를 구하기 위한 prior와 likelihood는 아래와 같다.

prior = Surrogate function,

likelihood = Acquisition function

그리고 두 함수는 BO가 더 효율적으로 solution을 찾기 위한 중요한 함수라고 할 수 있다.

그럼 두 함수를 어떻게 정의해야 더 효율적으로 Optimize 할 수 있는지 알아보자.

Surrogate function

1) GP regression

BO의 Surrogate function으로 GP regression를 사용하는 경우 Kernel에 따라 GP의 posterior mean, covariance가 달라질 수 있다.

Squared exponential kernel (Gaussian kernel)
: GP regression에 가장 흔히 쓰이는 Gaussian Kernel이다.

Matern kernel
: Gaussian kernel의 smoothness를 υ로 조절할 수 있어 많이 사용하는 Kernel이다.

2) Others : 그 외 Surrogate 함수로 사용할 수 있는 모델

- Random forest : 빠르지만 extrapolation에 취약한 단점이 있다.

- Neural networks

Acquisition Functions

사실 Surrogate function보다 Acquisition function을 잘 정의하는 것이 훨씬 중요하다.

앞서 예제에서 봤듯 Acquisition function a(x | D_1:t)은

Surrogate function의 mean과 variance 모두 큰 지점을 찾는 함수이자,

다음에 추가할 관측치(x_t+1)를 선택하는 기준이 되는 함수다.

1) Probability of improvement (PI)

가장 원천적인 방법은 현재 선택된 최대값 μ(x*)보다

새로운 관측치가 가질 수 있는 μ(x)가 더 클 확률(probability of improvement, PI)을 모두 살펴보는 것이다.

위 그림에서 x*는 현재까지 찾은 solution이다.

그리고 x는 또 다른 임의의 관측치인데, μ(x)가 μ(x*)보다 클 확률은 위 그림의 빗금친 구역의 면적 PI(x)이다.

이렇게 모든 관측치에 대해서 PI(x)를 구하는 과정을 반복하다 보면 시간은 좀 오래걸리더라도 optimal solution을 찾을 수 있다.

하지만 이 방법은 uncertainty가 매우 큰 구역(exploration)의 값은 잘 선택하지 않으려는 경향이 있기 때문에 sensitive를 조절할 수 있는 파라미터 ξ를 위와 같이 적용하는 것이 일반적이다. ( μ(x*)값을 조금 증가시켜주는 역할을 하는 하이퍼파라미터다.)

당연히 이런 비효율적인 방법은 쓰진 않지만 PI는 acquisition function의 목적을 가장 직관적으로 이해할 수 있는 원리다.

2) Expected Improvement

PI를 다시 정리하면, μ(x*)=y* 보다 큰 구역 전체를 적분한 것이 PI(x)였다.

반면 EI는, y가 y*보다 크다고 생각될 때(expected), 적분값을 acquisition function으로 인정한다.

그리고 마찬가지로 EI의 sensitivity를 조절하기 위한 ξ를 적용하면 위와 같이 일반화 할 수 있고,

Bayesian Optimization의 acquisition function으로 가장 많이 사용한다.
(굳이 위 식을 풀려고 하진 말자. 원리를 아는 것으로 충분하다.)

3) GP-UCB

EI 다음으로 많이 쓰는 acquisition function이다.

GP-UCB는 GP regression의 upper bound 최대값을 다음 관측치로 결정하는 방법이다.

(실제로 위 식은 mean + standard deviation을 의미한다.)

참고로 EI와 성능은 비슷하다.

5) Thompson Sampling

: GP에서 나온 함수 중 하나를 acquisition function으로 사용하는 방법이다.

Bayesian Optimization with Opensource

지금까지 Bayesian Optimization에 대해서 알아봤는데,

여기까지 따라왔다면 이제 Opensource를 사용할 자격(?)이 생겼다 할 수 있다.

BO는 상당히 오랜기간 연구를 거치면서 완성도가 높은 알고리즘인 만큼 아래와 같이 다양한 opensource들이 배포되어 있다.

SMAC
http://www.cs.ubc.ca/labs/beta/Projects/SMAC/

Hyperopt
http://jaberg.github.io/hyperopt/

Spearmint
https://github.com/JasperSnoek/spearmint/

Bayesopt
http://rmcantin.bitbucket.org/

Bayeso
https://github.com/jungtaekkim/bayeso

그 중에서도 역시 우리 수업에 도움을 주신 김정택 조교님의 opensource를 사용해서 간단한 하이퍼파라미터 튜닝을 해보았다.

- 모델 : GradientBoostingClassifier (sklearn)

- 최적화 대상

1) learning rate

2) n_estimator

3) subsampling

4) max_depth

import sklearn.datasets as skld
import sklearn.model_selection as sklms
import sklearn.ensemble as skle
import numpy as np
import matplotlib. pyplot as plt

# Gradient Boosting Classifier의 hyperparameter를 자동으로 튜닝
# learning_rate, n_estimators, subsample, max_depth
dataset = skld.load_digits() # MNIST와 유사한 digits
data = dataset.data
targets = dataset.target

X_train, X_test, Y_train, Y_test = sklms.train_test_split(data, targets, test_size=0.2, stratify=targets, random_state=42)
X_train, X_valid, Y_train, Y_valid = sklms.train_test_split(X_train, Y_train, test_size=0.2, stratify=Y_train, random_state=42)


def objective(hyps: list) -> float: 
    # hyps[0] -> learning_rate, real, log10, [-4, -1] -> 10^{learning_rate}
    # hyps[1] -> n_estimators, int, [50.0, 1000.9] -> int(n_estimators)
    # hyps[2] -> subsample, real, [0.5, 1.0]
    # hyps[3] -> max_depth, int, [3.0, 8.9]
    model = skle.GradientBoostingClassifier(
        learning_rate = 10**(hyps[0]),
        n_estimators=int(hyps[1]),
        subsample=hyps[2],
        max_depth=int(hyps[3])
    )
    model.fit(X_train, Y_train)
    score = model.score(X_valid, Y_valid)
    return 1.0-score

- 하이퍼파라미터 최적화

from bayeso import bo

ranges = np.array([
    [-4.0, -1.0],
    [50.0, 1000.9],
    [0.5, 1.0],
    [3.0, 8.9]    
])
model_bo = bo.BO(ranges, str_cov='matern52', str_acq='ei')
num_init = 5
num_iter = 10

hyps_train = []
loss_train = []

for _ in range(0, num_init):
    bx = model_bo.get_initials('uniform', 1)
    bx = bx[0]
    
    y = objective(bx)
    hyps_train.append(bx)
    loss_train.append([y])
    # random으로 num_init만큼 관측
    # = random search
    
for ind in range(0, num_iter):
    print('{} iteration'.format(ind+1))
    next_point, dict_info = model_bo.optimize(
        np.array(hyps_train), np.array(loss_train)
    )
    y = objective(list(next_point))
    print(dict_info)
    
    hyps_train.append(next_point)
    loss_train.append([y])
    
best_hyps, best_loss = utils_bo.get_best_acquisition_by_history(
    np.array(hyps_train), np.array(loss_train)
)
print(best_hyps, best_loss)
# learning rate, n_estimator, subsample. depth

- Bayesian Optimization 결과

[ learning rate n_estimator sub sample depth] loss

[ 10e-1.1389664 402.02611953 0.70940795 3.56200424] 0.017

Other Experiment

1) XGBoost를 튜닝하기 위한 BO vs. Random search 비교
※ learning rate, gamma, max_depth, n_estimators, min-child-weight

[http://krasserm.github.io/2018/03/21/bayesian-optimization/]

2) Soft-Voting in Ensemble

: Ensemble 모델의 Voting을 위해 weak learner의 weight를 BO 최적화

[J. Kim and S. Choi (2018), "Automated machine learning for soft voting in an ensemble of tree-based classifiers," ICML Workshop on AutoML]

Posts List

[머신러닝/딥러닝] 11-4. Bayesian Optimization

Bayesian Optimization

Bayesian Optimization