[머신러닝/딥러닝] 11-2. Gaussian Process Regression

Gaussian Process Regression

지금까지는 모델을 잘 만들서 단순히 예측만 했었는데, 이번에는 Prediction Uncertainty 까지 구할 수 있는 아주 강력한 regression 방법을 소개한다. 바로 Gaussian Process Regression이다.

Gaussian Process Regression은 대표적인 non-parametric regression이다. 직전 포스트인 [Kernel의 이해와 종류]에서 잠깐 언급했지만, Kernel을 사용했을 때 non-parametric하게 모델을 구할 수 있다고 했었다.

Gaussian Process 역시 Kernel을 활용한 non-parametric regression인데, 이번 포스트에서는 가장 간단한 non-parametric 모델인 Nadaraya-Watson Kernel Regression을 먼저 설명하고, Gaussian Process (이하 GP)를 설명하도록 한다.

Nadaraya-Watson Kernel Regression

Nadaraya-Watson estimator를 설명하기 전에, 직전 포스팅에서 다루었던 Kernel ridge regression의 모델을 다시 한번 살펴보면서 잠깐 Kernel의 특징을 살펴보자.

직전 포스트에서 Kernel ridge regression을 위와 같은 식으로 완성시켰다. 위 식의 α는 일종의 normalized 된 target value로 볼 수 있다. 그럼 Kernel 함수에 대해 살펴보기 위해 위 식을 전개해보자.

앞서 Kernel은 두 벡터의 유사도(similarity)를 표현한다고 했는데,
위 식을 잘 살펴보면 x*와 x1~xN 의 모든 유사도를 weighted sum하고 있다.

이렇게 모든 training example와의 유사도를 살펴보는 원리가 바로 Kernel regression의 공통적인 원리다.
그러다 보니 training example이 많으면 많을수록 연산량이 많은데, 이것 역시 non-parametric 모델의 특징 중 하나다.

그리고 Nadaraya-Watson Estimator(이하 N-W estimator)도 위 원리를 벗어나지 않는다.

위 식은 N-W estimator를 표현한 것이다. 여기서 Kernel 함수는 x*와 xn의 유사도가 높을수록 큰 값을 가진다. 

표기를 K(x*-x)로 쓴것은 별로 상관하지 말자. 만약 Kernel 함수로 위와 같은 Gaussian kernel을 사용한다면 어차피 (x*-x)에 의존하기 때문에 단순히 표기법의 차이다.

어쨌든 결국 위 식에서 분모는 normalization항이고, 분자는 weighted sum으로 Kernel ridge regression과 모양새가 크게 다르지 않음을 확인할 수 있다.

위 그림은 Gaussian Kernel을 사용하는 경우를 도식화 한 그림이다.

x* = x0로 주어졌을 때 위 그림의 주황색 영역이 kernel의 density distribution이다.
x0에서는 최대 similarity를 가지고, 좌우측으로 퍼지는 sample에 대해서는 낮은 similarity를 가지는 것을 확인할 수 있다. (초록색 선이 model을 fitting 한 것)

여기서 Gaussian Kernel의 h는 kernel의 표준편차를 의미한다. 즉, h가 커지면 kernel의 분산이 커지고, 주황색 영역이 옆으로 퍼지면서 멀리 떨어진 샘플의 similarity를 좀 더 높게 책정할 수 있다. 이 경우 초록색 선이 더 smooth해 지는 효과를 가진다.

Gaussian Process Regression(이하 GP regression)

※ C.E. Rasmussen and C.K.I. Williams (2006), "Gaussian Processes for Machine Learning", MIT Press

그럼 이제 본 포스팅의 핵심인 GP Regression을 살펴보자.

앞에서 잠간 언급했지만, GP Regression의 가장 큰 장점은 예측값의 신뢰구간 혹은 비신뢰구간(uncertainty)를 알 수 있다는 것이다. 위 그림은 GP regression으로 예측 된 mean function과 mean이 가질 수 있는 분산을 area로 표현해서 신뢰구간을 표현한 것이다. 어떤 원리로 저런 결과를 얻을 수 있을까? 심플한 예제를 한번 살펴보자.

위 5개의 (+)점을 지나는 함수는 몇 개나 될까? 아마 1개는 아닐 것이다.
위 그림처럼, 여러개의 함수를 그릴 수 있을 텐데, 공통점이 있다. 

바로 주어진 sample에서 각 함수의 편차는 매우 작다는 것이다. 반면 sample이 없는 미지의 영역에서는 함수들의 예측값이 큰 분산을 보이며 불안한 모습(certainty)을 확인할 수 있다.

이렇게 'Distribution of Function'을 구하는 것이 바로 GP Regression의 핵심이다.

Vanilla GP Regression

지금까지 배운 Regression은 파라미터 Θ를 optimize 하는 문제였다. 즉, 샘플 데이터 D가 주어졌을 때 P(Θ | D)가 최대인 Θ를 구하는 문제였다. 

반면 GP Regression은 Θ가 분포를 가지는 확률밀도 함수 f로 간주하기 때문에 여러개의 모델이 나올 수 있다. 즉, P( f | D), 데이터를 만족하는 함수들의 분포(posterior over function)를 구하는 문제다.

다만 functional distribution을 구하는 것이 쉽지 않은데, f(x)가 Gaussian distribution을 가진다고 가정하면 아래와 같이 쉽게 정의할 수 있다.

즉, 우리가 구하고자 하는 분포는 function 의 분포이기 때문에 mean 'function' μ(x)와 covariance 'function'=kernel function로 표현되는 Gaussian 분포를 가진다.

여기서 분산은 squared exponential kernel로, 모든 x pair들과의 similarity로 표현됨을 주목하자. 위 식을 잘 살펴보면 σf는 similarity의 크기를 조절하고 l은 similarity 분포의 폭을 조절한다. 즉, σf와 l을 어떻게 조절하느냐에 따라 functional covariance를 조절 할 수 있고 GP regression의 하이퍼파라미터라 할 수 있다.

위 파라미터에 대해서 다시 한번 정리하면

• l이 작을 수록 가까이 있는 샘플의 similarity를 더 높게 측정하기 때문에, 조금만 떨어져도 f(x)의 uncertainty가 요동친다.

• 반대로 l이 크면 멀리 있는 샘플의 similarity도 반영하기 때문에 f(x)의 uncertainty가 smooth해 진다.

• σf는 클수록 전체적인 similarity의 절대값을 높게 측정하기 때문에, f(x) uncertainty 절대적인 양이 커진다.

실제로 위 사례를 보면 

• l=0.3으로 작을 때, 샘플에서 조금만 멀리 떨어져도 uncertainty가 요동치는 것을 확인할 수 있다. 

• 반대로 l=3으로 클때는 sample이 없는 구역에서도 uncertainty가 안정적이다.

• σf=0.3 보다 σf=3를 가질 때 uncertainty가 존재하는 구역은 매우 큰 uncertainty를 가진다. 

※ 수업시간에는 위 원리를 선형대수로 증명했는데 본 포스팅에서는 GP regression의 원리 정도만 파악하고 넘어가기로 한다. Gaussian Process Regression에 대한 더 원천적인 설명은 Grio Learning 블로그를 참고하면 자세히 나와있으니 참고하자.

(user 입장으로써 너무 깊게 공부하기엔 GP regression은 좀 어렵다... 이정도만 알아도 충분할 듯)

GP regression은 이정도 수준으로만 다루고 정리해보자.

• GP regression은 function의 distribution을 표현하는 모델이다.
  그래서 posterior mean / variance를 구할 수 있다.

• posterior mean은 예측을 위한 함수로써 사용할 수 있고,
  posterior variance를 통해서 예측값을 얼마나 신뢰할 수 있는지를 알 수 있다.

• 통상 Kernel의 파라미터를 튜닝하는게 까다로운데 GP regression는 Kernel의 파라미터를 알아서 튜닝해주는 장점이 있다. (왠만한 라이브러리(ex. sklearn)에 다 구현되어 있다.)

• 다만, 모든 sample들의 similarity를 확인하는 kernel함수의 특성상 연산량이 많다.
  그래서 training example의 수가 적을때 가성비가 좋다.

※ GP regression을 마치기 전에 opensource library인 sklearn으로 GP regression을 구현한 예제를 보고 마치도록 한다.

import numpy as np

X_train = np.array([-3, -2, 0, 2])
Y_train = np.sin(X_train) + np.random.rand(X_train.shape[0])

X_all = np.linspace(-4, 4, 101)
y_all = np.sin(X_all)

Training sample로 4개 point를 만들자.

X_train = [-3   -2   0   2]

Y_train = [0.53   -0.52   0.41   1.75]

import sklearn.gaussian_process as sklgp

model_gpr = sklgp.GaussianProcessRegressor()
model_gpr.fit(np.expand_dims(X_train, axis=1), Y_train)
preds, stds = model_gpr.predict(np.expand_dims(X_all, axis=1), return_std=True)

GP regression을 sklearn으로 구현하는 것은 사실 위 3줄이면 충분하다.

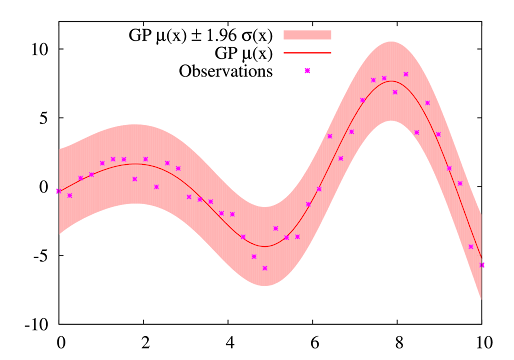
import matplotlib.pyplot as plt

plt.figure(figsize=(6, 8))
plt.plot(X_train, Y_train, linestyle='none', marker='x')
plt.plot(X_all, y_all, color='blue')
plt.plot(X_all, preds, color='red')
plt.fill_between(X_all, preds - 1.96 * stds, preds + 1.96 * stds, alpha=0.3, color='red')
plt.legend(['sample', 'real', 'preds', 'uncertainty'],)

간단하게 mean function과 covariance function을 위와 같이 그릴 수 있다.

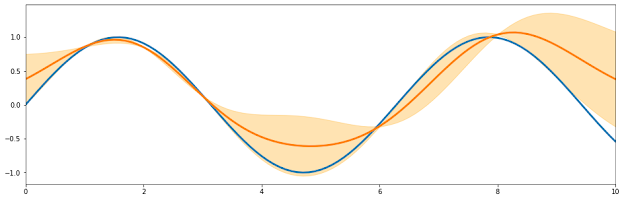
※ 물론 bayeso라는 우리의 김정택 조교님이 개발한 opensource로도 쉽고 더 정확하게 그릴 수 있다.

import bayeso
from bayeso.gp import gp
from bayeso.utils import utils_bo
import numpy as np
import matplotlib. pyplot as plt

X_train = np.array([[1.0], [2.0], [3.0], [6.0], [8.0],])
Y_train = np.sin(X_train) + np.random.randn(X_train.shape[0], 1) * 0.05

X_test = np.linspace(0.0, 10.0, 101)[..., np.newaxis]

Y_pred, sigma_pred, Sigma_pred = gp.predict_with_optimized_hyps(
        X_train, Y_train, X_test, str_cov='eq')

plt.plot(X_test, np.sin(X_test), lw=3)
plt.plot(X_test, Y_pred, lw=3)
plt.fill_between(X_test.flatten(),
                Y_pred.flatten() - sigma_pred.flatten(),
                Y_pred.flatten() + sigma_pred.flatten(),
                alpha=0.3, color='orange')
plt.xlim([np.min(X_test), np.max(X_test)])

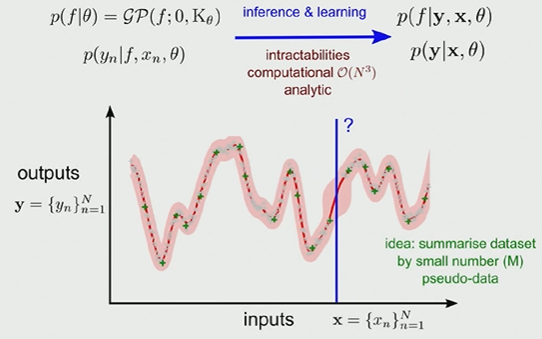
(Optional) Sparse GP regression

GP regression의 유일한 단점은 Kernel function에서 similarity를 구하기 위해 샘플 갯수 N^3 의 많은 연산량을 가진다는 것이다. 그래서 샘플이 많은 경우에는 효율적이지 못 할 수 있다.

하지만 만약 우리의 문제가 audio data를 함수로 표현하고 싶다면 문제가 달라진다. 왜냐하면 audio data의 수집 속도는 굉장히 빨라서 10초에도 수만개의 데이터가 수집될 수 있기 때문이다.

Sparse GP Regression은 전체 데이터가 아니라 pseudo-data M개를 을 선택한 후 문제를 풀고, 적게 선택한 만큼 발생한 bias를 어느정도 잡아주는 접근법이다.

pseudo-data를 어떤 것으로 선택할 것인지부터 고민해야하는데,(Sparse Pseudo-Input GP) 

결과적으로 Sparse GP Regression을 적용하면 M²N 번으로 연산량을 획기적으로 줄일 수 있는 효과가 있다.