[머신러닝/딥러닝] 11-1. Kernel의 이해와 종류

Kernel Methods

[데이터마이닝:SVM]과 [머신러닝/딥러닝:Linear Models] 에서 basis function(=feature map)과 kernel에 대해서 잠깐 언급한 적이 있었다. 이번 시간에 좀 더 자세히 알아보도록 하자.

Feature Map (=Basis function)

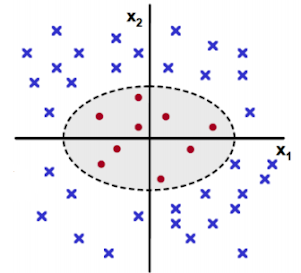
위 그림처럼 linear model f(X)로 샘플을 분류 할 수 없을 때는 어떻게 해야할까? 상식적으로는 non-linear model f(X)를 만들면 되겠지만, non-linear 문제를 푸는 것은 생각만큼 호락호락 하지 않다. 

이 때 발상을 좀 바꿔보면, input space X 를 linear model이 해결할 수 있는 형태인 feature space φ(X)로 만들면 문제를 해결할 수 있다. 마치 PCA를 이용해 새로운 feature를 찾는 것과 같은 원리다. 
※ 실제로 kernelPCA라는 알고리즘이 있다.

이 때 사용한 함수 Φ를 기저함수(basis function) 혹은 feature map이라고 한다. 
정리하자면, Φ는 비선형 특징을 가지는 Input space를 선형 특징을 가지는 Feature space로 변환해주는 함수다. Φ의 사용예를 몇 가지 살펴보자. 

만약 이런 데이터가 있다면 linear 한 방법으로는 절대 두 범주를 분류할 수 없다. 

하지만 input space X를 위와 같이 변형하면 linear 문제로 변환된다. 이 때 feature map 은 Φ(X) = (X, X²) 인 경우다. 한가지 예를 더 살펴보자.

이 데이터의 경우도 feature map 함수를 이용해서 분리가능하게 만들 수 있다.

확실히 feature map은 비선형문제를 선형화 할 수 있는 획기적인 방법이 될 수 있다. 하지만 여기서 첫번째 문제는 ① feature map을 찾는 것 자체가 매우 어렵다는 것이다.

두 번째 문제점을 말하기 전에 위 예제를 SVM으로 풀어보자.
※ SVM : 두 범주를 분리하기 위한 hyperplane을 찾는 모델. 아래 식이 생각나지 않아도 상관없다. 그냥 가볍게 넘어가자.

SVM은 두 범주간 거리(margin)를 최대화 하는 하이퍼플레인을 찾는 문제이며, margin을 최대화 하는 목적 함수는 아래와 같다.

하지만 input space가 linear하게 풀 수 없는 상태라면 아래와 같이 feature mapping 을 통해 풀 수 있다.

그럼 이제 문제를 풀 수 있는 상태가 됐다. 하지만 여기서 두번째 문제점이 나타나는데, 바로 ② Φ함수로 feature space를 만드는 연산량 + 내적 Φ(x_i)^TΦ(x_j) 연산량이 엄청나다는 것이다. 

Kernel

① Φ(x)를 정의하는 것 자체가 어려움

② Φ(x)를 정의한 후에도 문제를 풀기위한 연산량이 너무 많음

위 두 문제점을 동시에 해결하기 위해 고안된 Kernel의 목적은 바로

① 고차원 변환 + ② 내적 연산량 문제를 동시에 해결 하고자 하는 것이다.  

그리고 이미 증명된 다양한 Kernel들이 공개 되어 있다. 즉, 우리는 Φ가 어떤 함수인지는 몰라도 된다. 단지 Φ의 내적을 계산할 수 있는 Kernel을 가져다 쓰면 된다. 

다만, Kernel은 아래 Mercer's Theorem을 만족해야 한다.

• Kernel 함수 K 가 실수 scalar 를 출력하는 continuous function일 때,

• Kernel 함수값으로 만든 행렬이 Symmetric(대칭행렬)이고,

• Positive semi-definite(대각원소>0)라면,

• K(xi, xj) = K(xj, xi) = <Φ(xi), Φ(xj)>를 만족하는 mapping Φ 가 존재한다. 
    = Reproducing kernel Hilbert space

위 Mercer's Theorem을 만족하는 증명된 Kernel function은 아래와 같이 다양하게 존재한다. 

여기서 Kernel은 결국 두 벡터의 내적(inner product)이며, 기하학적으로 cosine 유사도를 의미하기 때문에 Similarity function 이라고도 불린다.
※ K(xi, xj) = xi와 xj의 유사도를 의미한다. (잘 기억해두자.)

그리고 이 함수들을 이용한 Linear technique를 Kernel Trick이라고 한다.

(Example) Kernel Ridge Regression

그럼 앞서 배웠던 Ridge Regression에 Kernel을 적용해서 한번 풀어보도록 하자.
※ 아래 수식이 기억나지 않는다면 지난 포스팅을 참고하자. 굳이 기억이 안나도 Kernel의 원리를 이해하는데는 문제없다.

위 식은 L2 regularization 을 위한 ridge regression 모델의 목적함수다.  위 목적함수를 풀기 위해 w로 편미분하는 과정을 거치면 최종적으로 파라미터 w는 아래와 같이 결정된다. 

만약 x가 linear 하기 풀릴 수 없는 상황이라면 Kernel trick을 사용해서 linear problem으로 만들 수 있다. 

즉, 위 식을 내적(inner product)으로 표현한 뒤 Kernel로 대체하기 위해 matrix inversion lemma에 따라 정리하면 아래와 같다.

여기서 Kernel K는 X가 주어지면 계산 될 수 있는 상수이기 때문에 α 역시 상수라 할 수 있다. 이제 여기서 구한 Θ를 이용해서 새로운 관측값 x*를 예측 해보자.

짠, 비선형 문제라 가정했던 non-linear ridge regression이 상수 벡터 α와 Kernel(x, x*)의 곱으로 Linear 하게 구할 수 있게 됐다. 물론 Φ를 우리가 직접 찾은게 아니라 Kernel만으로 풀었다.

그리고 또 중요한건, 기존에는 Θ를 학습하거나 계산했어야 했는데, Kernel ridge regression에서는 kernel 외에 파라미터가 없다. 

이렇게 non-parametric한 특징도 Kernel method의 중요한 특징이다.