[Data Mining] 10-2. SVM - Non-Separable case, 비선형 SVM

 

SVM (Support Vector Machine)

Non-Separable case

앞서 두 범주를 구할 수 있는 하이퍼플레인을 구하는 방법에 대해 배웠다.

만약 위 그림처럼 선형함수로 절대로 분리할 수 없는 관측치가 있는 경우에는 어떻게 하이퍼플레인을 정해야할까? 이런 경우를 non-separable case라 한다. 이렇게관측치가 non-separable 할 때 하이퍼플레인을 정의하기 위해 등장한 것이 여유변수(slack variable, ξ)이다.

여유변수(ξ)는 일종의 penalty인데, 그 크기는 위 그림에서 볼 수 있듯, 원래 있어야 할 범주의 위치와 현재 위치간 거리이다. 그리고 현실에서는 분명히 이런 관측치들이 많을 것이다. 그래서 모든 여유변수들의 합(Σ ξ)에 비례상수 C를 곱한값을 오분류 비용이라 정의한다.

따라서, 기존의 separable case의 SVM의 목적식이 non-separable case에서는 아래와 같이 변하게 된다.   

min Σj=1~p ^wj2/₂ + C Σi=1~Nξi

subject to.1 :  yi (Σj=1~pwjxjk + b) ≥ 1 - ξi  (i = 1, ... , N)

subject to.2 : ξi ≥ 0 (i = 1, ... , N)

위 목적함수는 마진을 최소화 함과 동시에 오분류비용도 함께 최소화하는 하이퍼플레인을 찾는다는 의미이다. 제약조건 역시 여유변수(ξ)로 인해서 일부 변했고, 여유변수는 음(-)의 값을 가지지 않는다는 제약조건이 추가됐다.

목적함수와 제약조건이 복잡해진 것 처럼보이지만, 추가된 항이 모두 선형항이기 때문에 Separable case와 정확히 똑같은 방법으로 풀이할 수 있다.

원 문제에 라그랑지안 변수를 도입하여 쌍대 문제화 하면 아래와 같고,
KKT condition을 적용해서 라그랑지안계수 α를 quadratic P/G으로 구할수 있다.

위 방법으로 구해지는 α와 ξ의 추정치에 따라 발생할 수 있는 경우를 해석하면 아래와 같다.

위 표에 근거하여 기하학적 α와 ξ의 추정치의 의미는 아래와 같다.

• α : 객체의 위치 결정
  → H1과 H2에 걸쳐져 있거나, H1-H2 사이에 위치할 수 있다.
  → H1-H2 사이에 위치하더라도 ξ에 의해 정상/오분류로 나뉠 수 있다.

• ξ : 객체의 예측 결과 
  → ξ ≤ 1이면 정확히 예측 한 것이다. (H1-H, H2-H간 거리가 1이기 때문)

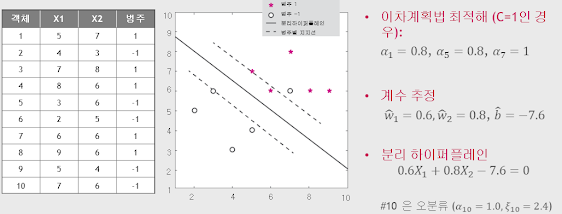
실제로 위 분석방법이 맞는지 예제로 확인해보자. (설명 생략)

비선형 SVM

지금까지는 두 범주를 선형함수로 분류하고자 하는 선형 SVM 모델에 대해 알아봤다. 하지만 위 상황처럼 선형으로는 분류할 수 없는데 비선형이라면 좋은 성능이 기대되는 경우는 어떻게 할까?

즉흥적으로 해결 방법을 고민하면 선형함수가 아니라 비선형함수를 하이퍼플레인으로 설정하면 될 것 같다. 그런데 그렇게 하지 않고, 역으로 관측치들을 변형시켜서 선형분리가 가능한 차원으로 만들 수 있다. 마치 2개의 변수로 이루어진 관측치를 PCA와 같은 기법으로 새로운 2개의 변수를 도출하는 것 처럼 차원을 변형하는 것이다.
※ 실제로 kernel PCA라는 기법이 있으며, kernel PCA를 SVM의 커널 기법으로 쓸 수 있다. 적용하면 위 그림처럼 선형분리가 가능한 차원으로 투영할 수 있다.

이런 기능을 하는 함수를 기저함수라 하며, 기저함수를 적용하면 아래와 같이 선형 하이퍼프레인으로도 비선형 관측치들을 분리할 수 있다.

f(x1, ... , xp) = Σm=1~M Φm(x1, ... , xp)wm + b  (M >> p)

Φm : 기저함수 (basis function)

※ 기저함수에 대해 추가적인 설명을 하자면, 기저함수는 위 그림처럼 비선형 관측치를 고차원으로 투영시키는 역할을 한다. 앞서 "새로운 차원을 도출한다."가 와닿지 않으면 위 그림을 떠올리면 쉽게 이해할 수 있다. (이런 행위를 Kernel Trick 이라고도 한다.)

그럼 이제 어떻게 Kernel Trick을 구현하는지 알아보자.

결론부터 말하면 우리가 Φ를 구하기 위해 애를 쓸 필요는 없다. Φ가 주어졌다고 가정하고, Φ들의 내적만 알면 관측치가 선형분리가 가능한지 판단할 수 있다. 이 때 Φ들의 내적(inner product)를 커널함수(Kernel function : 일종의 유사성 척도)라 한다. 주로 사용되는 커널도 함께 소개한다.

즉, 비선형 SVM은 비선형문제를 풀기위해 커널함수를 이용해 차원을 변환시켜 푸는 방법이다. 예측모형과 분류규칙은 아래와 같다.

f(x) = Σi=1~N $\hat{α}$i K(x, xi) + $\hat{b}$ 

f(x) > 0, 범주 1

f(x) ≤ 0, 범주2

비선형 SVM 에 2차 커널함수를 사용한 예제를 살펴보고 이번 챕터를 마친다.

앞에서 소개한 r차 다항 커널을 활용하는데 r=2로 셋팅하여 2차 커널로을 원 데이터에 적용하였다. 그리고 α의 제약조건을 0 ≤ αi ≤ C = 1 or 5 두가지를 설정하여 비교한 결과다. 확실히 C = 1일때 분류 결과가 좋다.

이렇게 모형에 지대한 영향을 미치는 파라미터를 하이퍼파라미터라고 하는데, 비선형 SVM에서도 제약조건 C / 어떤 커널함수를 쓸건지 등에 대해 신중하게 선택할 필요가 있다.

하지만 아쉬운건 이렇게 어떤 하이퍼파라미터를 써야할지에 대한 문제는 여간 어려운게 아니다. 그래서 통상 Grid Search와 같이 궁금한 경우의 수에 대해서 모두 모델을 만들어 보고 적절한 하이퍼파라미터를 사후에 택하는 전략을 취한다.