[빅분기] PART2. 빅데이터 탐색 - 통계기법의 이해 - 기술통계 (출제빈도 : 중)

        * 본문은 이기적에서 발행한 빅데이터분석기사 수험서를 공부하면서 작성된 글입니다. 시험 대비한 공부로, 암기가 필요한 부분을 요약/정리합니다.

※ Lecture note - 데이터마이닝 내용과 상당부분 중복됨으로 요약 정리

※ 계산문제는 책을 보고 별도로 복습 필요

PART2. 빅데이터 탐색

3. 통계기법의 이해

3-1. 기술통계 (Descriptive Statistics)

- 분석에 필요한 데이터를 요약하여 묘사, 설명하는 통계 기법

- 분석을 위해 단순히 데이터를 정리하는 행위 자체는 의미 없음 

 → 분석 전 데이터 특성을 찾아내 그 특성의 정량화를 통한 체계적 요약

- 기술통계의 종류 : ① 중심경향 ② 분산도 경향(흩어진 정도) ③ 자료의 분포형태(흩어진 모양)

1) 데이터 요약

- 데이터의 단순 정리가 아닌 분포가 가지는 특성을 찾아내 기본적인 특징을 수치로 정량화

- Chap.2 - Section 01. 기초통계량 문서 참조

2) 표본 추출

- 모집단(Population) : 연구, 실험의 결과가 일반화된 큰 집담, 정보를 얻고자 하는 대상의 전체 집합

- 표본 추출(Sampling) : 모집단으로 표본을 선택하는 행위

- 표본(Sample) : 원래 집단의 성질을 추축할 수 있는 자료

* 전수조사와 표본조사

① 전수조사 : 모집단 전체를 대상으로 조사 (ex. 인구조사). 정확하지만 인력과 예산이 비교적 많이 필요.

② 표본조사 : 모집단에서 표본을 추출하여 조사. 모집단을 대표할 수 있는 근거가 명확하다면 효율적.

   ※ 비용절감, 신속성, 조사규모가 크지 않기 때문에 심도 있는 조사 가능. 관리가 잘 되어 있어 정확도 보장

* 표본추출 오차(Sampleing Bias, sampling Error)

① 과잉 대표 : 중복선택 등이 원인 (모집단이 반복, 중복된 데이터만으로 규정되는 현상)

② 최소 대표 : 표본이 대표성을 나타내지 못하는 것이 원인 (표본 크기(size) 보다 대표성이 더욱 중요)

* 확률 표본추출 기법

- 모집단에 속하는 모든 추출단위에 대해 사전에 일정한 추출확률이 주어지는 표본추출법

- 표본자료로 부터 얻어지는 추정량의 통계적 정확도를 확률적으로 나타낼 수 있는 장점이 있음

① 단순무작위 추출(Simple Random Sampling)

 - 통계조사의 가장 기본적인 표본추출법

 - 모집단에서 무작위 추출, 독립적 선택으로 편향성(bias) 제거 , 난수 사용 하는 것이 기본

 - 모집단 내 조사단위수(N) 파악 후 원하는 표본수(n) 만큼 난수 발생 → 난수에 해당하는 표본 선택

 - 모집단에 대해 사전지식이 많지 않은 경우 시행하는 방법

② 계통추출(Systematic Sampling)

    (출처 : https://jennainsight.tistory.com)

 - 모집단에서 추출 간격(interval)을 설정하여 간격 사이에서 무작위로 추출하는 방법

 - N개인 집단에서 K라는 추출간격으로 뽑으면 N/K만큼의 표본이 선택됨 (=1/K 계통추출법)

③ 층화추출(Stratified Sampling)

    (출처 : https://jennainsight.tistory.com)

 - 모집단을 겹치지 않게 여러 층(strata)로 나누어 분할된 층별(stratum) 임의 표본을 추출하는 방법

 - 각 층은 비슷한 성질로 나누어져 있을 가능성이 큼 (표본이 구성원을 잘 대변할 수 있음)

   ex. 남성과 여성의 데이터가 3:2면, 층도 3:2로 나누어서 추출

 - 각 집단별 분석이 필요한 경우, 모집단 전체에 대한 특성치의 효율적 추론이 필요한 경우 사용

   (각 층별 추정 결과도 얻을 수 있기 때문)

 - 표본의 대표성 제고 및 조사관리가 편리하고, 조사비용이 절감됨

 - 층화변수(Stratification Variable) : 추출 단위가 어느 층에 속하는지 구분하기 위한 변수

   · 조사하고자 하는 변수와 밀접한 관련이 있는 보조변수가 되어야 함

   · 질적 층화변수 : 변수 값에 따라 층 구분

   · 양적 층화변수 : 층의 경계점을 나누는 방법 필요. 추정값의 분산을 최소화(최적경계점)

   · 표본의 배분

     1) 비례배분법 : 추출단위 수에 비례하여 표본크기를 배분 (층의 크기만 고려. ex. 남성2:여성3)

     2) 네이만배분법 : 층의 크기와 층별 변동의 정도를 동시에 고려. 변동이 큰 층에는 더 많은 표본 배정

     3) 최적배분법 : 추정량의 분산을 최소화시키거나 주어진 분산범위 하에서 비용을 최소화하여 배분하는 방법

④ 군집추출(Cluster Sampling)

    (출처 : https://jennainsight.tistory.com)

 - 모집단을 차이가 없는 여러 군집으로 나누어 일부 또는 전체에 대한 분석 진행

 - 표본집합이 이미 전체 모집단을 대표할 수 있어야 함

 - 모집단에 대한 구체적인 추출 방법론을 정하기 어려운 경우 사용하면 편리

 - 표본크기가 같은 경우 단순 임의추출에 비해 표본 오차가 커질 가능성이 있음

* 비확률 표본추출 기법

- 각 추출단위들이 표본에 추출될 확률을 객관적으로 나타낼 수 없는 표본추출법

- 모집단을 정확히 규정할 수 없는 경우, 표본오차가 크게 문제 안되는 경우, 조사에 앞서 새로운 개념 탐구에 활용

- 비용, 시간, 조사의 편리함 때문에 주로 사용

① 간편추출법(편의추출법, Convenience Sampling)

 - 응답자 선정에 있어 조사원 자의적인 판단에 따라 간편한 방법으로 표본 추출

 - 얻어진 표본이 모집단을 얼마나 잘 대변하는지 알 수 없음. 통계치에 대한 정확성 평가 어려움

   (ex. 지나가는 사람들을 대상으로 여론조사 하는 경우)

② 판단추출법(Judgement Sampling)

 - 조사자가 나름 지식과 경험을 통해 모집단을 잘 대표한다고 여겨지는 표본을 주관적으로 선정

 - 마찬가지로 조사자의 주관적 판담임으로 추정치 정확성을 객관적으로 평가할 수 없음

 - 표본의 크기가 장은 경우에 조사의 오차는 추정량의 분산이 좌우

   (ex. 전국 학생 성적 평균을 알아보기 위해 특정 몇 학교를 나름대로 선택하는 경우)

③ 할당추출법(Quota Sampling)

 - 조사목적과 밀접하게 관련된 대상자 연령, 성별과 같은 변수에 따라 부분집단으로 구분하고

   모집단 부분집단별 구성 비율과 표본의 부분집단별 구성비율이 유사하게 표본을 선정

 - 비용이 적게 들고 손쉽기 때문에 단기간 조사 할 때 유용

   (ex. 학생 서비스 만족도 조사할 때 기존 자료에 의거 성별 구성비율을 알아본 다음 그 비율에 따라 표본을 할당)

④ 눈덩이추출법(Snowball Sampling)

 - 접근이 어렵거나 추출틀(Sampling Frame)의 작성이 곤란한 특정 집단에 대한 조사에 활용

 - 해당 집단에 속한 것을 아는 사람에게 다른 사람을 소개받아서 조사를 진행 (표본이 눈덩이처럼 점점 커짐)

   (ex. 폭력조직원의 약물사용 실태를 조사할 경우, 대학교수들의 금융토자자산에 대한 인식 조사 등)

3) 확률분포

- 기술 통계 : 분석에 필요한 데이터를 요약하고 묘사, 설명하는 통계 기법

- 추측(추론) 통계 : 표본에 내포되어 있는 정보를 이용해 모집단에 대한 과학적인 추론을 하는 통계 기법

- 확률, 확률분포 : 모집단에 대한 추측 및 추론이 얼마나 정확한지에 대한 논리적 타당성을 제시하는 도구

* 확률의 개념

- 통계적 현상 : 반복하여 관찰하거나 혹은 집단 안에서 대량으로 관찰해 고유의 법칙을 찾아내는 것이 가능한 현상

- 확률 실험 : 같은 조건 아래 반복의 수를 늘리면서 규칙성을 찾아내는 것

 ① 확률 (Probability)

  - 통계적 현상의 확실함의 정도를 나타내는 척도. 랜덤 시행에서 어떠한 사건이 일어날 정도.

  - 수학적 확률 : P(A) = n(A) / n(S) → A사건의 확률 = A경우의수 / 전체경우의 수

    ※ 각 사건이 일어날 가능성이 동등할 때 (ex. 주사위, 카드뽑기)

  - 통계적 확률 : p = rn / n → 사건의 통계적 확률 = 사건 발생 횟수 / 총 횟수 (반복 & 수렴)

    ※ 실제로는 사건 가능성이 동일하지 않아 수학적 확률로 구하기 어려움. 확률을 상대도수로 추정해야함.

       n회의 시행에서 사건이 r회 일어났다고 하면 상대도수 = r/n으로 정의

 ② 사건 (Event)

  - 동일한 조건으로 여러차례 반복하는 실험이나 관측 = 시행, 시행의 결과로 나타나는 것 = 사건

  - 어떤 사건의 확률은 그 사건에 포함되어 있는 각 결과 발생 확률의 합  ex. 동전던지기

 ③ 표본공간 (Sample Space)

  - 통계적 실험에서 모든 발생 가능한 실험결과들의 집합

  - 전사건 = 표본공간 / 공사건 = 아무것도 포함하지 않는 사건 / 근원사건 = 하나의 결과를 포함하는 사건

  - 표본공간이 S인 확률 실험에서 사건은 S의 부분집합

 ④ 확률의 기본 성질

  - 0 ≤ P(Ai) : 사건A가 발생할 확률은 항상 0 이상

  - P(S) = 1  : 표본공간 S 사건이 발생할 확률 = 1 (사건은 모두 표본공간(S) 내에서 발생)

  - P(Ai ∪ Aj) = P(Ai) + P(Aj) - P(Ai ∩ Aj) 

  - P(A) ≤ 1, P(Φ) = 0 : 존재하지 않는 사건이 일어날 확률 = 0

  - if Ai⊂Aj, P(Ai) ≤ P(Aj)

 ⑤ 조건부 확률 : P(A | B) = P(A ∩ B) / P(B) → B가 일어났다는 조건하에 다른 사건 A가 일어날 확률

 ⑥ 결합확률 (확률의 곱셈) : P(A) X P(B) = P(A ∩ B) → A, B가 동시에 일어날 확률

    ※ 조건부 확률에서 A,B가 독립적이면 P(A | B) = P(A) 인 것을 활용한 식

 ⑦ 총확률정리 (Total Probability Rule) : P(B) = Σ P(B | Ai) P(Ai)

  - 임의의 사건 B의 확률을 k개의 조건부 확률을 이용해 구하는 방법

 ⑧ 베이지안 정리 ※ 관련글 : [AI] Probability

  - 총확률정리 활용, k개의 상호 배타적인 사건(A1 ... Ak)에 대한 사후확률(Posterior Prob.)를 구할 수 있음

  - P(Ai) 는 미리 주어진 사전확률(Prior), 사건 B라는 새로운 사건 발생시 P(Ai|B)를 구할 수 있음 (사후확률)

  - P(Aj) = P(B|Aj)P(Aj) / P(B) = P(B|Aj)P(Aj) / ΣP(B|Aj)P(Ai)

  ex. 흡연자 30%가 기관지에 이상있음. 실제로 90%가 이상반응나옴. 이상이 없어도 이상나타날 확률은 10%

      임의의 흡연자가 검사했을 때 이상반응이 나타났지만 실제로 이상이 없을 확률은?

  해설) A1은 기관지에 이상이 있을 사건,  A2는 이상이 없을 사건, B는 이상반응이 나타날 사건

        P(A1) = 0.3,   P(A2) = 0.7,  P(B|A1) = 0.9,  P(B|A2) = 0.1

        ※ P(B|A1) : 기관지에 이상이 있고 + 검사결과 이상반응이 나타날 확률

           P(B|A2) : 기관지 이상 없는데 + 검사결과 이상반응이 나타날 확률

        P(B) = P(B|A1)P(A1) + P(B|A2)P(A2) = 0.9 * 0.3 + 0.1 * 0.7 = 0.34

        검사결과 이상이 있는 사람이(B) 실제로는 이상이 없을(A2) 확률 

        P(A2|B)를 베이지안 정리로 구할 수 있음

* 확률변수

 ① 확률변수(Random variable) : 사건 시행 결과(확률)를 하나의 수치로 대응시킬 때의 값(확률값, X로 표기)

  - 확률 변수 X가 특정값 x를 가질 때 확률은 P(X=x)로 표기 (ex. 동전2개 던질 때 앞면이 2개 나올 확률 P(X=2))

    ※ X(뒤-뒤) = 0, X(앞-뒤) = 1, X(뒤-앞) = 1, X(앞-앞) = 2 라고 했을 때

 ② 확률변수의 종류

  - 이산(Discrete)확률변수 : 확률변수가 취할 수 있는 값의 수가 유한한 변수 ( ex. X = {0, 1, 2, 3} )

  - 연속(Continuous)확률변수 : 취할 수 있는 값의 수가 무한한 변수 (ex. 키, 몸무게, 시간)

* 확률분포

- 수치로 대응된 확률변수의 개별 값들이 가지는 확률값의 분포

- 확률변수가 취할 수 있는 구체적인 값을 확률공간상의 확률값으로 할당함

  ex. 두개의 주사위를 던져서 나오는 점들의 합 P(Y=y), y=1~12

      P(Y=2) = 1/36, P(Y=3)=2/36, P(Y=4)=3/36, ... P(Y=12) = 1/36

 ① 이산확률분포 (Discrete Probability Distribution)

  - 확률변수가 취할 수 있는 값의 수가 유한한 확률분포

  - 확률질량함수(Probability Mass Function) : 모든 x에 대해서 0 ≤ f(x) ≤ 1, Σf(x) = 1

 ② 연속확률분포

  - 확률변수가 취할 수 있는 값의 수가 무한한 확률분포

  - 확률밀도함수(Probability Density Function) 

     : 모든 x에 대해서 0 ≤ f(x) ≤ 1, ∫f(x) dx = 1,  P(a < X < b ) = ∫a~b f(x) dz

 ③ 확률분포함수 (Probability Distribution Function, 확률함수, PDF)

   출처 : https://thebook.io/080246/0401/

  - 확률변수가 취할 수 있는 구체적인 값 하나하나를 확률공간상의 확률값으로 할당해주는 함수

  - 이산확률분포함수 : 확률변수가 이산적인 확률분포를 가지는 함수

  - 연속확률분포함수 : 확률변수가 연속적인 확률분포를 가지는 함수

* 확률변수의 기댓값과 분산

 ① 기댓값(Expected Value)

  - 각 확률변수가 특정 값을 가질 확률을 가중치로 확률변수의 결과값을 평균화한 값

  - 이산확률변수의 기대값 E(X) = Σxf(x),  f(x) = 확률질량함수

    ex. 주사위를 한번 던졌을 때 기댓값 E(x) = 1*1/6 + 2*1/6 + ... + 6/1/6 = 3.5

  - 연속확률변수의 기대값 E(X) = ∫x*f(x)dx,  f(x) = 확률밀도함수

    ex. 구간 [0, 1]에서 연속인 확률변수 X의 확률밀도함수 f(x) = 1이라면

        X의 기대값 E(X) = ∫x*f(x) dx = ∫0~1 x dx = 1/2

  - 기댓값은 선형성 ( E(aX+b) = aE(x)+b ), 덧셈법칙( E(X+Y) = E(X) + E(Y) )이 성립하고,

     곱셉법칙은 일반적으론 성립하지 않지만 두 변수가 독립이면 성립함. 

 ② 분산(Variance)

  - 확률분포의 산포(퍼짐정도)를 나타내는 측도. 기대값에서 떨어진 거리의 제곱의 기댓값(평균)임. Var(X)로 표시

  - 이산확률변수의 분산

    Var(X) = Σ(x-μ)^2 f(x) = E(X^2) - {E(X)}^2

  - 연속확률변수의 분산

    Var(X) = ∫(x-μ)^2 f(x) dx = E(X^2) - {E(X)}^2

  - Var(aX) = a^2 Var(X)

  - Var(X+b) = Var(X)

  - Var(aX+b) = a^2 Var(X)

  - Var(X+Y) = Var(X) + Var(Y) + 2Cov(X, Y)

* 이산확률분포의 종류 (이미지 출처 : Wiki 백과)

- 베르누이 / 이항 / 다항 / 보아송 / 기하 / 음이항 / 초기하 분포

 ① 베르누이 분포 (Bernoulli, X~Bern(x, p) )

  - 결과가 성공 아니면 실패, 두 가지로 귀결되어 나오는 이산확률 분포

 ② 이항분포 (Binomial, X~B(n, p))

  - 베르누이 시행을 n번 독립적으로 시행할 때 성공횟수를 X로 정의한 이산확률분포

 ③ 다항분포 (Multinomial)

  - 여러 개의 값을 가질 수 있는 독립확률변수들에 대한 확률분포

  - 여러 번의 독립적 시행에서 각각의 값이 특정 횟수가 나타날 확률을 정의하는 분포

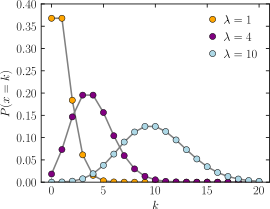
 ④ 포아송분포 (Poisson, X~Pois(λ) )

  - 단위 시간 안에 어떤 사건이 몇 번 발생할 것인지 표현하는 이산확률분포

  - 단위 공간이나 면적에도 적용 가능 (ex. 은행창구에 도착한 고객의 수, 책 한 페이지당 오탈자의 수)

  - X를 단위시간당 발생건수라고 하면 포아송분포는 평균 사건 발생수 λ에 의해 유도 됨

    → 포아송분포는 기댓값과 분산이 동일하게 정의(λ)

  - 이항분포는 n, p라는 두개의 모수에 유도되지만 포아송분포는 λ 하나로 정의

    → 이항분포를 포아송분포로 근사시켜 확률을 구하는 경우도 있음

       → 이상확률변수 X는 n이 무한이 커지고 성공확률 p가 매우 작다면 λ=np(이행분포의 기댓값) 으로 근사

 ⑤ 기하분포 (Geometric)

  - 베르누이 시행에서 처음 성공까지 시도한 횟수를 분포화한 이산확률분포

  ex. 시험에 합격할 확률이 0.7일 때 4번만에 붙을 확률 P(X) = 0.3*0.3*0.3 * 0.7 = 0.0189

 ⑥ 음이항분포 (Negative Binomial)

  - x번의 베르누이 시행에서 k번째 성공할 때까지 계속 시행하는 실험에서의 확률

  ex. 7전 4선승제 게임에서 7번 경기만에 우승이 결정될 확률

 ⑥ 초기하분포 (Hypergeometric)

  - 비복원 추출에서 N개 중 n개를 추출했을 때 원하는 것 k개가 뽑힐 확률

  ex. 불량품 선별

* 연속확률분포의 종류

- 연속균등 / 지수 / 정규 / 표준정규 / 감마 / 카이제곱 / 스튜던트t / F 분포

 ① 연속균등분포 (Continuous Uniform, X~U(a, b) )

  - 분포가 특정 범위 내에서 균등하게 나타나 있는 경우

  ex. 버스가 5분간격으로 출발, 학생이 임의로 정류장에서 버스를 기다리는 평균 시간과 3분 이상 기다릴 확률

 ② 지수분포 (Exponential, X~Exp(β) )

  - 사건이 서로 독립적일 때, 일정 시간 동안 발생하는 사건의 횟수가 포아송 분포를 따른다면,

    다음 사건이 일어날 때까지의 대기시간(β 혹은 1/λ)에 대한 확률이 따르는 분포 

  - 포아송 분포는 단위 시간단 발생하는 사건의 횟수를 관측 (횟수)

    지수분포는 사건이 일어날 때까지의 대기 시간을 관측 (대기시간)

 ③ 정규분포 (Normal, X~N(μ, σ^2)

  - Carl Friedrich Gauss에 의해 정의되어 가우스분포(Gaussian Distribution)이라 부르기도 함

  - 표본을 통한 통계적 추정 및 가설검정이론의 핵심.

  - 실제 사회적, 자연적 현상에서 접하는 여러 자료들의 분포가 정규분포를 띔

  - 확률밀도 상 평균을 중심으로 대칭이며 평균과 표준편차에 의해 완전히 결정

  - 전체 면적은 1, 정규분포곡선은 X축에 닿지 않음. (-∞ < X < +∞)

 ④ 표준정규분포 (Standard Normal, X~N(0, 1))

  - 정규분포의 확률밀도함수 그래프의 밑부분 면적 구하는 것은 매우 어려움

    + 정규분포의 위치는 평균과 표준편차에 따라 달라짐

  - 평균=0, 표준편차=1 이 되도록 변환하면 계산이 편해짐 → 표준정규분포

 ⑤ 감마분포 (Gamma)

  - 두 개의 매개변수를 받으며 양의 실수를 가질 수 있는 분포

  - 지수분포나 포아숭분포 등의 매개변수와 연관이 있음

  - 확률변수 X = 포아송과정 (β=θ)에서 k개의 사건이 발생할 때까지의 대기시간

  - (k, θ) = (1, θ)인 경우 감마분포는 지수분포와 동일

  - 신뢰성 이론이나 수명시험에 유용하게 사용

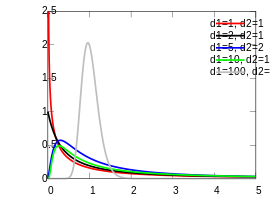
 ⑥ 카이제곱분포 (Chi-Squared, X~X^2(k))

  - k개의 서로 독립정인 표준정규확률 변수(X1 ... Xk)를 제곱한 다음 합해서 얻어지는 분포

  - 카이제곱분포의 매개변수는 k로 자유도(Degree of Freedom)을 뜻함, 기대값 = k, 분산 = 2k

  - (k/2, θ) = (k/2, 2) 인 감마분포는 카이제곱분포와 같음. 신뢰구간이나 가설검정에 주로 사용

 ⑦ 스튜던트 t 분포 (Student t, X~t(n-1) )

  - 정규분포의 평균 측정 시 주로 사용하는 분포. 모양은 Z-분포와 유사. (t=0에 대하여 대칭)

  - 자유도 ν가 t-곡선의 모양을 결정. (ν = 표본크기 n - 1)

    ※ 자유도 : 자료집단의 변수 중에서 자유롭게 선택될 수 있는 변수의 수

 ⑧ F 분포 ( X~F(k1, k2) )

  - 두 개의 확률변수(V1, V2)의 자유도가 각각 k1, k2이고, 서로 카이제곱분포일 때 자유도가 k1, k2인 F-분포

  - F검정이나 분산분석 등에 주로 사용되는 분포함수

4) 표본분포 (Sampling Distribution, Finite-sample Distribution)

- 크기 n의 동등한 확률로 추출된 확률표본(Random Sample)의 확률변수의 분포

* 모집단 분포와 표본분포

 ① 모집단의 모수(parameter)

  - 모집단의 특성을 나타내는 특성값 (모집단의 평균 μ, 모집단의 표준편차 σ)

 ② 표본의 통계량

  - 표본집단의 특성을 나타내는 특성값 (표본집단의 평균 X_bar, 모집단의 표준편차 S)

* 표본평균의 표본분포

- 표본집단에서 얻을 수 있는 모든 표본평균값(X_bar)을 확률변수로 하는 확률분포

* 표본평균의 표본분포 통계량

① 표본평균(X_bar)의 표본분포의 평균 = 모집단의 평균(μ)

② 표본평균의 표본분포의 표준편차 = σ√(n) ~ N(μ, {σ√(n)}^2) 정규분포 ※ σ =모집단의 표준편차(제곱하면 분산)

③ 표준오차(표본분포의 표준편차, 퍼짐정도) σx_bar 

 - 표본평균(X_bar)의 표준편차를 의미. (Standard Error of the Mean, 혹은 Standard Error)

 - 표본집단의 크기 n이 모집단 크기의 5% 이상 시 유한 모집단 수정계수를 사용해 표준편차 산출

* 중심극한정리 (Center Limit Theorem)

독일한 확률분포를 가진 독립 확률변수 n개의 평균의 분포는 n이 적당히 크다면 정규분포에 가까워진다는 정리

① 린데베르그-레비(Lindeberg-Levy) 중심극한정리

 - 확률변수 X1...Xn들이 서로 독립 + 같은 확률분포 + 확률분포의 평균과 표준편차가 유한하다면

   평균 S의 분포는 기대값 μ, 표준편차 σ√(n)인 정규분포 N(μ, σ√n)에 수렴

② 중심극한정리의 의미

 - 모집단의 분포가 무엇이든 상관없이 표본의 수가 큰 표본분포들의 표본평균의 분포가 정규분포를 이룸

 - 정규분포는 표준정규분포로 변환 가능하므로 추론이 쉬움

* 표본평균의 표준화

① 표본평균 X_bar는 정규분포의 확률변수로서 평균이 μ, 표준오차 σ√(n)이므로 표준화는

   Z = (X_bar - μ) / σx_bar = (X_bar - μ) / σ√(n) ~ N(0, 1)

② 표준화 Z는 확률변수인 X_bar(표본평균)가 

   모평균인 μ로부터 표본평균들의 표준편차인 표준오차의 몇 배만큼 떨어져 있는 가를 표시

③ 표준화 Z를 통해 표준화 한 후 표준정규분포표를 이용해 확률을 찾을 수 있음

* 표본비율 (Sample Proportion)

- 크기가 N인 모집단으로부터 표본크기 n 표본 추출, 조사 결과가 성공 혹은 실패로 구분될 때,

  n개의 개체 중 성공으로 나타나는 개체 수의 비율

  ※ 모비율 : 모집단에서 성공으로 나타나는 개체 수의 비율. 모집단의 특성

* 표본비율의 표본분포 (Sampling Distribution of Sample Proportion)

- 모든 표본들에 대한 표본비율 값의 확률분포

① 표본분포에서의 평균과 표준오차

 - 표본의 크기가 클 때 중심극한정리에 의해 표본분포는 모비율 평균(P)이고 표준오차 σp = √(pq/n)

   ※ q = 1 - p,   n 은 표본크기

 - 모비율이 극단적으로 0 혹은 1에 가깝거나 표본의 크기가 적을때를 제외하면 np ≥ 5 와 nq ≥ 5 모두 성립

② 표본비율의 표본분포

 - 표본비율의 표준화는 표본평균의 표준화와 동일 개념