[강화학습] 5. Temporal-Difference

Temporal-Difference

• MC는 model-free지만, 전체 episode을 다룬 다음에야 value update가 가능한 단점이 있다.

• 반면 DP는 time-step로 value update가 가능하지만, model이 주어져야 한다.

Temporal Difference Learning

TD는 MC와 DP의 장점을 취하고 단점을 극복하기 위한 아이디어이다.

• model을 몰라도 되는 (model-free) MC의 장점

• final outcome을 기다리지 않아도 time-step마다 value update가 가능한 DP의 장점

즉, TD는 MC처럼 dynamics 모델 없이 experience만으로 학습하고, DP처럼 return이 아닌 estimate를 사용해서 value를 evaluate, update한다. (bootstrap)

※ 그래서 TD는 central & novel RL method라 평가되고 있다.

DP vs. MC vs. TP의 관계는 강화학습을 공부하면 자주 나오는데, 결국 모두 GPI에서 약간 변형된 형태라고 볼 수 있다. 

다만 다른점은 prediction문제를 어떻게 해결하느냐의 차이이다.

이번 포스팅에서도 DP, MC 포스팅과 같이, 

이번에는 TD가 π의 가치를 평가하는 prediction problem, optimal π를 찾는 control problem을 어떻게 다루는지 알아보도록 하자.

TD Prediction

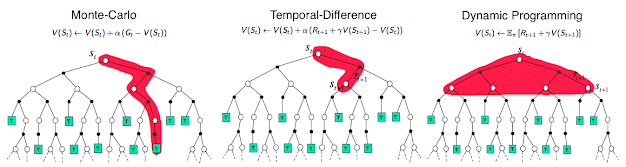
앞서 설명했듯, MC vs. DP vs. TD는 value evaluation방법만 조금 다른 한끗차이 알고리즘이다. 그리고 그 것을 설명하는 것은 위 그림으로 한방에 해결된다. 한번 정리해보자.

(b) Dynamic P/G

가장 먼저 배운 Dynamic P/G때는 (b) 식의 expectation을 풀어서 위와 같은 bellman equation을 증명해냈다. 

※ p(s', r | s, a) * r = R,     p(s', r | s, a) * γvπ(s') = γG(s)

(a) Monte Carlo

하지만 dynamics p(s', r | s, a)를 모르면 위 방법을 쓸 수 없기 때문에, MC는 가장 기본적인 expected value의 정의 (a)에 기반하여, sample mean으로 value를 evaluate했다.

bandit은 과거의 가치, MC는 미래의 가치를 이용해서 가치를 정하고 update했다.

(c) Temporal difference

하지만 MC의 결정적인 단점은 episode의 끝까지 가지 않는 이상 value evaluate를 구할 수 없다는 것이었고, 이 문제를 해결하기위해 TD는 return Gt를 다른 관점으로 바라본다.

위 식의 파란부분은 Gt에 해당하는 항인데, Gt는 action에 의해 얻은 reward R_(t+1)과 action을 통해 변한 state S_(t+1)의 가치를 discounting 하여 더한 것과 같다.

결론적으로 [ ]괄호 안은 S_(t+1)과 S_(t)의 가치 차이(temporal difference 혹은 TD error)라고도 할 수 있고, 이 방법을 TD(0) 혹은 one-step TD라고 부른다.

즉, TD는 episode의 끝까지 가지 않고 t시점의 에러인 temporal difference를 마치 gradient처럼 사용하여 V(St)를 update하는 방식을 보이고 있다.

그리고 위 식을 잘 보면 V(St)를 예측하기 위해 V(St+1)를 estimate하는 bootstrap의 원리를 따른다는 것을 확인할 수 있다.

[출처 : MC러닝, 강화학습 포스팅의 교재인 Sutton 노트 review를 잘 정리해놨다.]

pseudo code를 보면, DP와 같이 bootstrapping 기반으로 prediction하고 있는것을 확인할 수 있다.

아래는 TD(0)의 backup diagram을 보여준다.

즉, TD(0)는 모든 episode가 끝난 후에 value function을 estimate하는 것(like MC)이 아니라, every step마다 update 해 주는 것을 의미하며, 이 때 estimated value function을 사용해 update하는 bootstrap의 원리를 가진다.

위 과정을 위와 같이 표현할 수 있으며,

두 estimate 간의 차를 TD error라 부른다.

이제 최소한 지금까지 배운 MC, DP, TD의 backup diagram을 이해할 수 있어야 한다.

• MC의 value function은 episode가 끝났을 때 진행된다.

• TD(0)는 1-step마다 update된다.

• GP는 모든 가능한 successor에 대해 expectation한다.

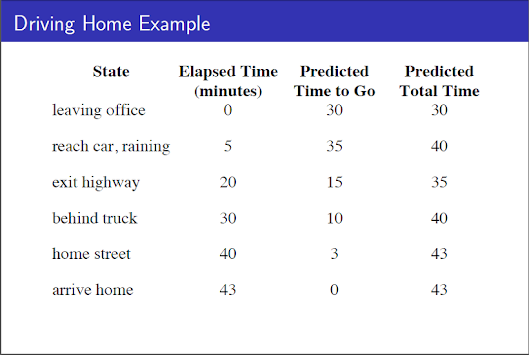
Driving Home example을 이용해 TD와 MC를 간단히 비교해보자.

직장을 출발해서 집으로 돌아오는데 생길 수 있는 상황들을 state로 한 문제이다.

이 때 다음 state로 이동한 실제 시간이 reward이며, agent는 이를 바탕으로 value function을 update해야한다.

이 때, MC와 TD가 value function을 학습한 결과는

• MC의 방법을 따르는 agent는 episode가 모두 끝나야 update하는 반면,

• TD의 방법을 따를때는 final outcome은 모르지만 매 step마다 얻은 reward를 바탕으로 value function을 update하는 모습을 볼 수 있다.

• 현실에 대입하면, "생각보다 고속도로를 빨리 나왔으니 10분 일찍 도착할 것 같다." 혹은 "비가 왔으니 조금 더 걸릴 것 같다."고 prediction하는 것과 같다.

지금까지 배운 것을 토대로 Advantage of TD를 살펴보면,

• model을 몰라도 되고, (vs. DP)

• episode 끝까지 안가도 되기 때문에 update가 더 빠르다 (vs. MC)

• 그리고 이론상 correct answer에 converge하도록 guaranteed되어 있으며, (technically sound)

• 실시간으로 learning 하는 일종의 incremental learning이다.

Optimality of TD(0)

incrementally learning(step by step)은 횟수도 많고 수렴하는데도 힘들다. 왜냐하면 1-step에 존재한 bias들이 converge 속도와 방향에 방해가 되기 때문이다.

그래서 mini-batch와 같은 개념을 batch updating이라고 한다. 즉, 1개 sample마다 update하는 것이 아니라 적당한 수를 뽑아서 update하는 것이다. (mini-batch의 개념은 머신러닝/딥러닝에서 다루었으니 여기서 다루진 않는다. )

TD Control

TD Prediction에 대해서 알아봤으니, DP, MC와 마찬가지로 optimal policy를 찾는 TD Control에 대해서도 알아보자. 그리고 앞 포스팅에서 잠시 맛봤던 On-policy control과 Off-policy control에 대해서도 이번에 자세히 알아보도록 하자.

SARSA : On-policy TD Control

앞 포스팅에서 잠깐 소개했듯, Control 단계에서는 여느때(GPI)와 마찬가지로 qπ(s, a)를 estimate하는데, 현재까지 찾은 policy π에 의존해서 update하는 것이다.

즉, 위와 같이 현재 state St에 action At를 취해 나온 reward Rt+1을 활용해 St_1을 평가하고, 새로운 state에 다시 action At+1을 취해 reward Rt+2를 얻는 방식을 반복한다고 할 수 있다. 

그리고 이런 원리를 가진 가장 대표적인 on-policy control방법이 바로 S.A.R.S.A 이다.
(= Q를 estimate하기 위해 필요한 것은 현재 S에 action A을 취해 받은 R, 이로 인한 새로운 state S와 next action A)
(만약 t+1의 state가 terminal 이면, t+1의 action value Q는 0으로 취급한다.)

위 pseudo code에서 Sarsa는 action을 선택하는데 ε-greedy를 사용했지만, 다른 방법을 사용해도 무방하다.

여기서 주목할 것은, action A를 state S로부터 ε-greedy하게 결정했고,(behavior policy)

S'으로부터 A'을 결정할 때도 ε-greedy하게 결정했다는 것이다. (target policy)

Q-learning : off-policy control

off-policy control은 앞 포스팅에서 간단히 설명했지만, target policy를 선택할 때, 현재까지 update 된 π와 무방하게 선택한다.

자율주행 자동차에 대해 예를 들면, 안전한 episode에서 결정된 policy보다 새로운 도전적인 policy에 대해서도 학습할 필요가 있다. 즉 exploratory policy와 함께 optimal policy가 선택되어야 한다는 것이다. 이것이 off-policy control의 목적이며, 대표적인 알고리즘은 Q-learning이 있다.

즉, next action을 결정하는 단계(target policy)에서 π와 무방하게 취할 수 있는 모든 action을 평가하는 방법이다.

실제 pseudo code에서도 behavior policy (ε-greedy)와 target policy (max = greedy)가 다른 것을 확인할 수 있다.

위 예제는 절벽(Cliff)에 떨어지지 않기 위한 최단거리를 찾는 RL의 예제이다.

늘 모든 action을 ε-greedy하게 평가해서 절벽 근처에 가지 못하는 Sarsa와 달리,

Q-learning은 좀 더 도전적(exploring)으로 최단 경로를 찾는 것을 확인할 수 있다.

Expected Sarsa

[sarsa]

expected sarsa는 sarsa가 next state의 action value를 sampling했다면 (high variance)

[expected sarsa]

expected sarsa는 expected action-value를 사용해 sarsa의 variance를 낮춘 방법이다.

즉, Q-learning이 모든 action-value들의 maximum value를 취했다면, Expected Sarsa는 현재 policy를 따랐을 때 expected value를 고려해 action-value function을 evaluate한다.

Double Q-learning

지금까지의 control algorithms에는 maximization function이 많이 들어있었다.

• Q-learning에서는 가능한 모든 action의 maximum

• SARSA에서는 ε-greedy를 통한 argument maximum

그런데 maximum value를 estimate해야하기위해 estimate value를 maximize한다? 이게 과연 옳은 방법일까?

위 문제의 경우, 가장 왼쪽으로 갔을 때 action value의 평균은 -0.1일 지라도, 1의 분산이 있기 때문에 action의 maximization은 양수일 수 밖에 없다. (=maximization bias)

그래서 항상 maximum value를 학습하는 Q-learning은 수렴 속도가 초반에 느릴 수도 있고, 심지어 optimal policy에 수렴하지 못하는 문제가 발생한다.

그래서 고안된 것이 바로 Double Q-learning이다.

Double Q-learning은 update 된 Q2에 다시 한번 action을 취해보고, 그 가치가 Q1보다 높은지 낮은지 ε-greedy하게 결정하는 원리이다.

Summary

• TD(0) method는 one-step learning이다.

• control 단계의 on-policy 대표적인 예는 Sarsa가 있다.

• off-policy의 대표적인 예는 Q-learning과 Expected sarsa가 있다.

• Double Q-learning은 maximization bias를 피하기 위한 방법이다.

다음 포스팅에서는 TD(0)가 one-step learning이었다면, 이의 일반화된 버전, 즉 n-step TD에 대해서 알아보도록 하자.