Finite Markov Decision Process
가장 idle하게 RL을 구현하는 방법이다. 가장 기초가 되는 개념인만큼 추후에도 계속 활용이 되니 잘 알아두도록 하자.
Example: Grid world
grid로 표현된 world에서 로봇이 이동하는데, deterministic 하게 이동하는 것이 아니라 stochastic 하게 이동할 수 있다. MDP을 이해하기 가장 쉬운 예제로 이후에도 자주 나올 예정이다.
- State s: 로봇의 x, y위치
- Action a: 상/하/좌/우
- Reward r(s, a) : s에서 a를 취했을 때 얻을 보상
- Transition function p(s', r | s, a) : s에서 a를 취했을 때 r을 얻으면서 s'으로 갈 확률(=environment model = dynamics)
이번 포스팅에서는 s, a, r을 명확하게 표현할 수 있는(Finite) 문제를 MDP로 풀어보도록 한다.
MDP (Markov Decision Process)
MDP는 순차적으로 행동을 결정(sequential decision making)하는 문제를 classical한 수식으로 나타낸 것이다.
이 때 학습 혹은 행동 결정자를 에이전트(agent), 그리고 agent와 상호작용하는 것을 환경(environment)라 한다. 그리고 이 둘은 서로 상호작용하며 정보(state, reward)를 주고 받는다.
위와 같이 Environment는 Action을 받아 새로운 상태 S가 되고, 그에 따른 보상 R을 받는다.
물론 간단한 문제라면 이것으로 충분하지만, 현실 문제는 그리 간단하지 않다.
어떤 Action을 했더라도 꼭 원하는 방향으로 가지 않을 수 있다.
(Grid world의 로봇에게 Up의 action을 줘도 Down으로 오동작할 수 있다.)
그래서 Dynamic를 아래와 같이 정의한다.
잘 보면 이전 state나 action에 대한 정보가 없고, 오직 직전 state의 action을 가지고 현재 state와 reward가 결정되는 것을 확인할 수 있다.이러한 상태를 Markov property를 가지고 있다고 말하며,
"현재 상태가 주어졌을 때 미래와 과거는 독립적이다는 가정을 의미한다."
※ 앞서 이근배교수님의 AI수업에서 P(Alarm), P(Fire)는 원래 dependent 한 사건이었지만 직접적인 원인인 P(smoke)가 주어진다면 두 사건은 independent한 상태가 된다는 것과 같은 의미다.
그럼 Markov property를 만족한다면 아래의 state transition probability pij를 표현할 수 있다.
위 식만 보면 이해가 잘 되지 않지만 아래 예제를 보면 직관적으로 이해할 수 있다.위 예제를 통해 pij는 state i에서 state j로 가는 확률을 표현함을 알 수 있다. (ex. p[s1 → s2] = 0.4)이렇게 transition probability가 주어지고, reward, state가 finite 하다면 아래와 같이 dynamics, expected reward도 쉽게 계산할 수 있다.
위 예제는 s0에서 a1을 취했을 때 얻을 수 있는 reward를 구하는 모습을 보여준다.Reward, Return, Episode
RL의 Goal은 Reward를 최대화하는 action sequence를 찾는 것이다.
그렇기 때문에 Reward를 어떻게 정의하느냐에 따라 문제는 달라질 수 있다.
- Game : win +1, lose -1, otherwize 0
- Maze(미로) : each time step -1 before escape
- Balancing : maintaining balance +1
Episode는 start에서 시작해서 terminal에서 끝난 full sequence를 의미한다. (Episodic Task)
다만, terminal state 없이 영구히 진행되는 episode는 Continuing Task라 한다.
그리고 RL의 목적은 sequential action을 planning 하는 것인데, 이 때 agent의 목표는 앞으로 받을 Reward의 총합을 Maximize 하는 것이다.
이 때 '앞으로 받을 보상'을 expected Return 이라고 하며, episodic task에서의 Return은 아래와 같다.
다만, 이 때 얻을 수 있는 보상에 대해 가중치를 줄 수가 있다.
예를 들면 가까운 미래에 얻을 수 있는 보상은 의미가 크고, 먼 미래에 얻을 보상의 크기를 작게 두는 것이다. 이 개념이 discounting이다.
이 개념을 적용해 expected discounted Return을 정의 하면 아래와 같다.
위 식의 discount rate γ는 [0, 1]사이의 값을 갖기 때문에 먼 미래의 Reward의 가치를 exponential 하게 감소시키는 것을 볼 수 있다.
또한 t시점의 Return은 t+1시점의 Return과 Recursive 한 관계로 표현할 수 있다.
※ γ를 극단적으로 가졌을 때
- γ=0 : Myopic → 한치앞의 미래만 보는 문제
- γ=1 : Farsighted → 먼 미래의 보상에도 큰 기대를 하는 문제
위에서 정의한 Return을 Episodic / Continuing Task 모두에서 사용하기 위한 Unified Notation을 정의하면 아래와 같다.
우린 앞으로 위 식을 이용해서 Return을 구할 예정이다.
Policy, Value functions
Policy π(a | s) 는 action을 어떻게 선택할지를 결정하는 중요한 확률 함수이다.
마찬가지로 어떤 Policy를 따랐을 때, 기대되는 Reward를 계산하는 Value function도 매우 중요하다.
정확하게는, Value function은 agent가 앞으로 얼마나 보상을 받을지(expected return)를 표현하는 함수이며, 아래 2가지가 있다.
※ value function에는 항상 π가 붙어있다. 즉, policy에 dependent한 것이다.
state-value function
state s에서 policy π에 따라 쭈욱 행동할 때, 기대되는 가치(return)를 의미한다.→ state s의 가치를 매긴 것
그리고 state s의 가치는 s에서 할 수 있는 모든 action들에 대한 가치를 반영하기 때문에 아래와 같이 표현할 수도 있다.
즉, vπ(s)는 state s에서 할 수 있는 모든 action들에 대한 value (action-value)의 평균이다.
action-value function
state s에서 여러개의 action을 취할 수 있을텐데, 이 때 특정 action a를 했을 때 얻을 수 있는 가치를 의미한다.→ state s에서 할 수 있는 action a의 가치를 매긴 것
이때 action은 dynamics에 따라 stochastic한 특징을 가진다. p(s', r | s, a)
그리고 action을 통해서 바로 얻을 수 있는 가치가 있고, p(s', r | s, a) * r
action을 통해 이동한 state s'의 가치 p(s', r | s, a) * γv(s')가 있다.
이 두가지 가치를 합친것이 action a의 총 가치라 할 수 있으며, 아래와 같이 표현할 수 있다.
두 함수에서 볼 수 있듯, state-value, action-value는 서로 coupled 되어 있다.
Bellman Equation (BE)
BE는 state-value와 action-value가 coupled된 함수를
state-value는 state-value의 liner function, action-value는 action-value의 linear function으로 표현한다.
※ 본 포스팅에서 Bellman equation의 증명은 다루지 않는다.
BE for state-value function
앞서 정의한 state-value function에 action-value function을 대입하면 아래와 같은 새로운 state-value function을 구할 수 있다.
위 식을 잘 살펴보면, 모든 action value를 policy의 확률로 평균 내는 것을 확인할 수 있다.
책에서는 이 방정식을 위와 같은 다이어그램으로 표현하며 backup diagram이라 부른다. (backup이라 부르는 이유는 RL에서 핵심인 backup operation이나 update의 기초를 형성하는 관계를 그린 다이어그램이기 때문이라고 한다.)이 다이어그램을 해석해보면, s의 가치(state-value)는 s의 다음으로 올 수 있는 모든 state들의 가치를 모두 알아야 구할 수 있다는 것이다. (bootstrapping)
BE for action-value function
예제를 하나 풀어보자.
- state : 25 state (5x5)
- action ∈ {↑, ←, ↓, →}
- policy = uniform random : π(a | s) = {1/4, 1/4, 1/4, 1/4}
- stochastic uncertainty 가 없는 dynamics : p(s', r | s, a) = 1
- reward
- 움직일 수 없는 벽으로 갈 때마다 -1, 나머지는 +0
- s2에 위치하면 +10 얻으면서 s22로 강제 이동
- s4에 위치하면 +5 얻으면서 s14로 강제 이동
- discounting = 0.9
위와 같은 environment가 있을 때, 각 state의 value (state-value : vπ)를 BE로 구해보자.
모두 다 구하기는 많고, s1, s2의 state-value만 한번 구해보면, 아래와 같다.
실제로 v1을 구하기 위해서는 v2, v6가 필요하고, v2를 구하기 위해서는 v22가 필요한 것을 확인할 수 있다.- π(a | s) : s에서 a ∈{↑, ←, ↓, →} 를 선택할 각 확률은 모두 1/4로 동일하다
- p(s', r | s, a) : uncertainty가 없다고 했음으로 1
- s1에서 ↑, ←로 가면 벽으로 이동했음으로 reward는 -1
- s1에서 ↓, →로 가면 다음 셀로 이동하며 reward는 +0
- 이 때 discounting에 의해 v2의 state-value x 0.9가 작용함
- s2는 어느 방향으로 가든 s22로 강제 이동함으로 모든 보상은 +10
이런 방식으로 모든 state의 가치를 구할 수 있다.
위 결과는 {1/4, 1/4, 1/4, 1/4}의 random policy π0를 가졌을 때 state-value를 의미한다.추후에 Dynamic Programming에서 배우겠지만 state-value를 구했다면 π0를 π1으로 improve 시킬 수 있다. (policy improvement, PI) 위 그림은 greedy method를 통해 policy를 improve시킨 결과이다.
Bellman Optimality Equation (BOE)
앞서 예제에서 확인했듯, {↑, ←, ↓, →}로 이동할 policy π0 = {1/4, 1/4, 1/4, 1/4}로 했을 때 state-value vπ0를 구할 수 있다.
→ π0을 평가하기 위해 vπ0을 구한 것이기 때문에 policy evaluation이라고 한다.
그리고 잠깐 언급했듯, vπ0를 이용해서 greedy method를 적용하든, ε-greedy method를 적용하든 해서 π1으로 improve시킬 수 있다. (=1 iteration)
→ vπ0을 통해 π1으로 improve 시켰다고 해서 policy improvement라고 한다.
※ policy evaluation / improvement는 추후에 dynamic programming에서 더 자세히 다루도록 한다.
물론 π1도 optimal 하지 않을 수 있기 때문에 지금까지와 동일한 방법으로 π1을 적용해 새롭게 vπ1 을 구할 수 있고, 마찬가지로 π2로 improve시킬 수 있다 (=2 iteration)
이 과정을 반복하다 보면(policy iteration) 더이상 update되지 않는 순간이 발생하는데, 이 때를 optimal policy, optimal value function이라 한다.
결국 BOE는 최적의 policy를 찾도록 해 주기에 RL을 풀었다고 할 수 있지만 위 수식을 직접적으로 푸는 것은 좋지 않다. 왜냐하면 BOE는 exhaustive search(모든 경우의 수를 다 보는 탐색 방법)과 같기 때문이고, 그 마저도 아래 3가지 가정이 성립되었기 때문이다.
- environment의 dynamics를 정확히 알고 있다.
- Markov property를 만족한다.
- exhaustive search가 가능한 성능 좋은 컴퓨터가 있다.
AlphaGo가 RL의 가장 유명한 예라고 할 수 있는데, 바둑은 사실 dynamic가 명확하고 Markov property를 만족하기 때문에 2개 가정은 별 문제가 없었을 것이다.
하지만 바둑 게임의 경우의 수가 어마어마하기 때문에 exhaustive search를 한다는 것은 사실상 불가능 했을 것이다.
그래서 이를 근사(approximate)할 방법이 필요한데, 다음 포스팅에서 대표적인 근사 방법인 Dynamic Programming을 다루도록 한다.
물론 2번째 가정인 Markov property도 사실상 현실 문제에는 적용되기가 어렵다. 왜냐하면 현재 일어나는 사건은 직전이 아니라 훨씬 예전의 사건으로부터 기인했을 수 있기 때문이다. 그래서 이 문제를 해결하기 위한 방법도 추후에 Monte Carlo Methods 등으로 다룰 예정이다.
Summary
- 강화학습은 목표를 위해 agent와 environment가 상호작용하면서 학습하는 것을 말한다. 이 때 상호작용하는 요소는 action, state, reward가 있다.
- Policy는 상태에 따라 agent가 선택하는 action의 확률적인 규칙을 말한다.
- agent의 목표는 앞으로 받을 보상(Return)의 양을 최대화 하는 것
- 전이 확률(transition probabilities)와 함께 정의가 잘 되면 Markov decision process(MDP)라고 부른다.
- Return은 에이전트가 최대화하기위해 노력하는 미래 보상들의 합이다.
expected value로 표현하며 상황에 따라 discount factor가 포함된다.
- 상호작용이 끝나는 지점이 있다면 episodic task
계속 된다면 continuing task
- 각 state마다 policy의 가치함수(value function)가 할당되어 있다. 그리고 value function은 expected return으로 표현된다.
- 최적의 가치 함수(optimal value function) 또한 각 상태마다 할당 되어 있으며, 어떤 policy가 이룰 가장 큰 expected return이다.
- 최적의 가치함수에 따른 policy는 optimal policy가 된다.
- 벨만 최적 방정식은 최적의 가치함수가 만족해야하는 일관성 조건으로 이를 만족하는 해를 구하면 최적의 가치를 구할 수 있으며, 마찬가지로 최적의 정책을 구할 수 있다.
- 환경을 완전히 안다면(complete knowledge) 환경에 대한 완벽한 모델을 구성할 수 있지만, 완전히 알지 못한다면(incomplete knowledge) 구성할 수 없다.
- 설령 완전히 안다고 해도 큰 문제일수록, tabular 방법으로는 풀 수 없다. 따라서 근사(approximate)를 해야한다.









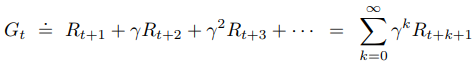
















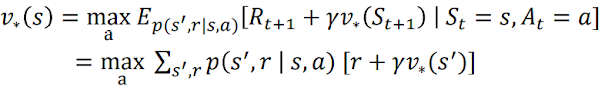



![[빅분기] PART4. 빅데이터 결과 해석 - 분석결과 해석 및 활용 - 분석결과 활용 (출제빈도 : 하)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj2tCMzQ5D2rhqkDfbphh9LKohFnYl3Df8LahM8gskD0BNHA5jX1MLhVIuG78S5IdyrrQrB60ygONq5FvYBLzrUnJrOhKpTfTFzZP0TFS_lZDipN44DhIq8FfFfnieRwTSzDCXvKacFQWvlcETOaoxXS0KNSFdN3apRHi5ReqUer7jCvbIFp2tj8Gmqci3S/w680/%EB%B9%85%EB%8D%B0%EC%9D%B4%ED%84%B0%20%EA%B5%AC%EC%B6%95%EB%B0%A9%EB%B2%95%EB%A1%A0%20%EB%B9%84%EA%B5%90.png)
0 댓글