[컴퓨터비전] 16. Image Warping

Image Warping

Filtering이 이미지 픽셀의 range를 변경시키는 연산자였다면,

Warping은 이미지의 domain을 변경시키는 연산자이다.

가장 간단한 연산자인 scaling, rotation matrix는 아래와 같다.

모든 픽셀에 위와 같은 연산자를 통해 scale을 조정하거나 이미지를 회전 시킬 수 있다. 

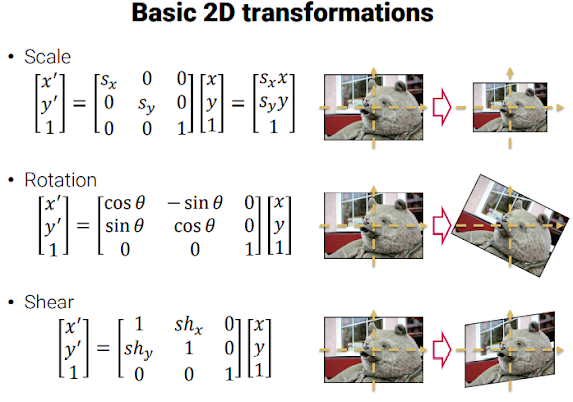
이런 2x2 matrix를 일반화 시켜 2D linear transformation으로 표현하면 Scale / Rotation / Shear / Mirror 등 다양한 연산을 수행할 수 있다.

특히 이렇게 일반화 했을때 위와 같이 복합연산을 합쳐서 1개의 matrix로 표현(composition)할 수 있는 등의 이점이 있다. 

그리고 2차원 공간의 좌표의 표현을 3개 coordinate로 표현(homogeneous coordinates) 하면 아래와 같이 3개 기본연산자를 정의할 수 있다.

그리고 translation 연산까지 포함하는 일반화된 연산자는 아래와 같다.

위 식을 보면 Cartesian (2x2) coordinate에서는 translation 항을 2D matrix로 표현하지 못했던 반면 Homogeneous coordinate에서는 2D matrix안에 모든 연산자를 포함시킬 수 있다.

좀 더 특별한 연산자로는 Projective 연산자가 있다.

이 연산자는 특히나 중요한 연산자인데,

2장의 사진을 찍었을 때, 두 사진간의 차이를 통해 관계를 projective 연산자로 정의 할 수 있다.

지금까지 언급한 translation operator들을 정리하면 위와 같다.

그럼 이제 이미지를 translation을 시키는 방법은 알았는데, 그럼 지금 이미지가 어떤 연산을 통해 변형됐는지를 파악해보자.

이 때 transformation 별로 필요한 point수가 다른데,

translation은 1점만보고 x, y축 값을 비교하면 되고,

similarity(translation+rotation+scaling)은 3개의 point

projective는 4개의 점이 필요하다.

각각 다른 정보를 필요한 이유는 마치 미지수의 수만큼 방정식이 필요한 연립방정식이 필요한 만큼 translation의 자유도(degree-of-freedom)만큼 point가 있어야 recovering translation이 가능하다.

이번 포스팅에서는 이미지의 변환에 대해서 알아봤는데 다음 포스팅에서 활용 방법에 대해 다뤄보도록 하자.