[머신러닝/딥러닝] 9-1. Convolutional Neural Network(CNN)

Convolutional Neural Network

지금까지 Real number로 구성된 feature를 입력으로 받는 딥러닝 모델에 대해 알아봤다.

CNN은 이미지를 딥러닝 모델에 적용하기 위해 고안된 알고리즘이고, CNN을 공부하다 보면 위 그림과 같은 표현을 자주 마주칠 것이다. 위 그림 중 그나마 친숙한 부분은 오른쪽에 Fully Connected layer 뿐인데, 이번 시간을 거치면 이제 논문이나 기사에서 위와 같은 그림을 보더라도 충분히 해석할 수 있을 것이다.
(대부분의 그림은 「AI VISION 라온피플」의 블로그에서 가져왔다. 설명도 훨씬 자세하게 잘 되어 있으니 시간있으면 정독하는 것도 좋을 듯하다.)

Multi-layered network의 한계

[3x3 이미지를 9x1 벡터로 변환한 예제]

일단 이미지를 입력으로 하는 딥러닝 모델을 만들 수 있을까? 결론은 아무 문제 없이 가능하다. 왜냐하면 이미지는 수많은 픽셀로 이루어져있는 Matrix이고, 픽셀은 0~255사이의 숫자로 표현되기 때문이다. 이걸 일자로 쭉 펼치면 결국 실수로 구성된 벡터이기 때문에 아래와 같이 딥러닝을 적용할 수 있다. 

다만 문제점은 모델 사이즈가가 엄청나게 클 것이다. 만약 위 그림처럼 16x16의 작은 이미지를 일자로 쭉 펼치면 256개의 feature를 가지는 벡터가 된다. 즉, input layer의 노드가 256개나 필요하다. 그리고 100개 노드를 가진 hidden layer 1층만 쌓아도 학습될 파라미터 수는 약 3만개나 된다. 

만약 이미지의 해상도가 더 높고, 깊은 신경망을 이루게 된다면 파라미터의 수가 수천만개는 쉽게 뛰어넘는다. 이 쯤 되면 학습속도도 문제지만 수렴은 할 수 있을지부터 의심해 봐야 한다. 그럼 예상가능한 몇 가지 문제점을 알아보도록 하자.
※ 참고로 통상 파라미터 수 x 10배 만큼의 학습 데이터가 필요하다고 하니 데이터 마련부터 아마 큰 고난이 있을 듯 하다.

가장 큰 문제점은 이미지의 기하학적 특징(topology)를 전혀 학습하지 못한다는 것이다.

위 예제는 똑같은 문자 'A'가 입력된 것 처럼 보이지만, 실상은 그렇지 않다.
딥러닝 입장은 loss에 어떤 pixel이 영향을 미쳤는지 back propagation 할 것이다. 예를 들어 왼쪽 그림처럼 3, 4번째 feature가 흰색, 5, 6번째 feature가 검정색이면 'A'라는 글자를 예측하도록 학습됐다고 하자. 그럼 오른쪽 경우는? 똑같은 'A'지만 3, 4, 5, 6이 모두 검정색이다. 그럼 딥러닝 입장에서는 이 두가지를 분류할 방법을 찾기가 굉장히 어려워진다.

그런데 이미지는 위와 같이 언제 어떤 형태든 가질 수 있다. 그렇기 때문에 각 픽셀과 loss간의 gradient를 구할 것이 아니라 이미지 자체의 topology를 학습할 수 있어야 한다.

만약 이 문제를 해결하려면 굉장히 많은 'A'를 표현하는 이미지가 필요하다. 그리고 데이터가 많아진 만큼 학습시간도 엄청나게 오래걸릴 것이다.

결과적으로 Fully Connected multi-layered neural network를 통해 이미지를 학습하려고 하면 아래 문제점을 마주하게 된다.

학습시간   /   신경망의 크기   /   변수의 갯수

위 문제점들을 해결하면서 이미지를 학습하기 위한 딥러닝 구조가 바로 CNN이다.

CNN (Convolutional Neural Network)

CNN이 가장 처음 발표된 시기는 1989년 Yann LeCun의 논문(Backpropagation applied to handwritten zip code recognition)이지만 1998년 Yann LeCun, Yoshua Bengio의 논문(Gradient-based learning applied to document recognition), 2003년 Behnke의 논문(Hierachical Neural Networks for Image Interpretation) 이후로 대중화 되었다. 

CNN은 크게 3개 구조로 구성되어 있다.

• Convolution : Filter를 이용해 이미지의 특징을 추출(feature extraction)하는 단계

• Sub-sampling : topology 변화에 영향을 받지 않도록 하는 단계

• Fully connected layer : 학습된 특징들로 분류하는 단계

지금부터 각 단계가 어떻게 연산되는지 알아보도록 하자.

1) Convolution

사실 이미지와 filter(혹은 kernel)의 합성곱(convolution)연산으로 이미지의 특징을 뽑는 것은 CNN 이전에 영상처리에서 널리 사용되는 방법이다.

[Andrew Ng 강의 자료(COURSERA)]

위 그림은 가장 전형적인 vertical edge를 추출하는 과정이다. 실제로 6x6 이미지에 3x3필터를 합성곱 해서 edge의 정보가 추출된 4x4 이미지가 만들어 졌다. (4x4 이미지를 그려보면 vertical edge를 표현하는 실선이 그려질 것이다.)

[Blur, Shift filter 적용 예]

[emboss, impressing filter 적용 예]

그 외에도 Corner를 찾거나, Blur, Emboss 효과를 주는 filter들이 이미 경험적으로 개발되어(hand written filter) 영상처리에 사용되고 있다.

CNN 이란 이름에서 확인할 수 있듯, CNN의 핵심 기능은 Feature를 추출하는 Convolution layer에 있다. 그리고 Convolution layer의 목적은 바로 Filter를 학습하게 하는 것이다.

즉, Hand written filter처럼 Filter내에 들어가는 숫자를 사람이 지정하는 것이 아니라, Filter값들이 Back propagation을 통해 optimized 될 수 있게 하는것이 CNN의 핵심이다. 그럼 Convolution layer에서 어떤 일이 벌어지는지 확인해보도록 하자.

[출처 : A Comprehensive Guide to Convolutional Neural Networks, towards data science]

위 그림과 같은 6x6이미지에 3x3 filter를 합성곱 해보자.
※ filter = [ [1, 0, 1], [0, 1, 0],  [1, 0 1] ]

합성곱 연산은 말로 설명하는 것 보다 위 그림을 보고 이해하는 것이 빠른데, 굳이 설명하자면 모든 원소들끼리의 곱을 더하는 연산자가 바로 합성곱이다. 위 그림에서는

(1x1) + (1x0) + (1x1) + (0x0) + (1x1) + (1x0) + (0x1) + (0x0) + (1x1) = 4

의 Scalar값이 계산되어서 Convolved Feature에 저장된 모습이다.

동일하게 Filter를 오른쪽으로 한칸씩, 아래쪽으로 한칸씩(stride=1) 이동시키면서 합성곱 연산을 하면 위와 같은 Convolved Feature를 구할 수 있다.

만약 이미지가 흑백(1 channel)이 아니라 RGB(3 channel)이여도 문제없다. 위 그림처럼 3x3x3 filter를 사용하면 1개의 scalar 값을 얻으면서 이동할 수 있다.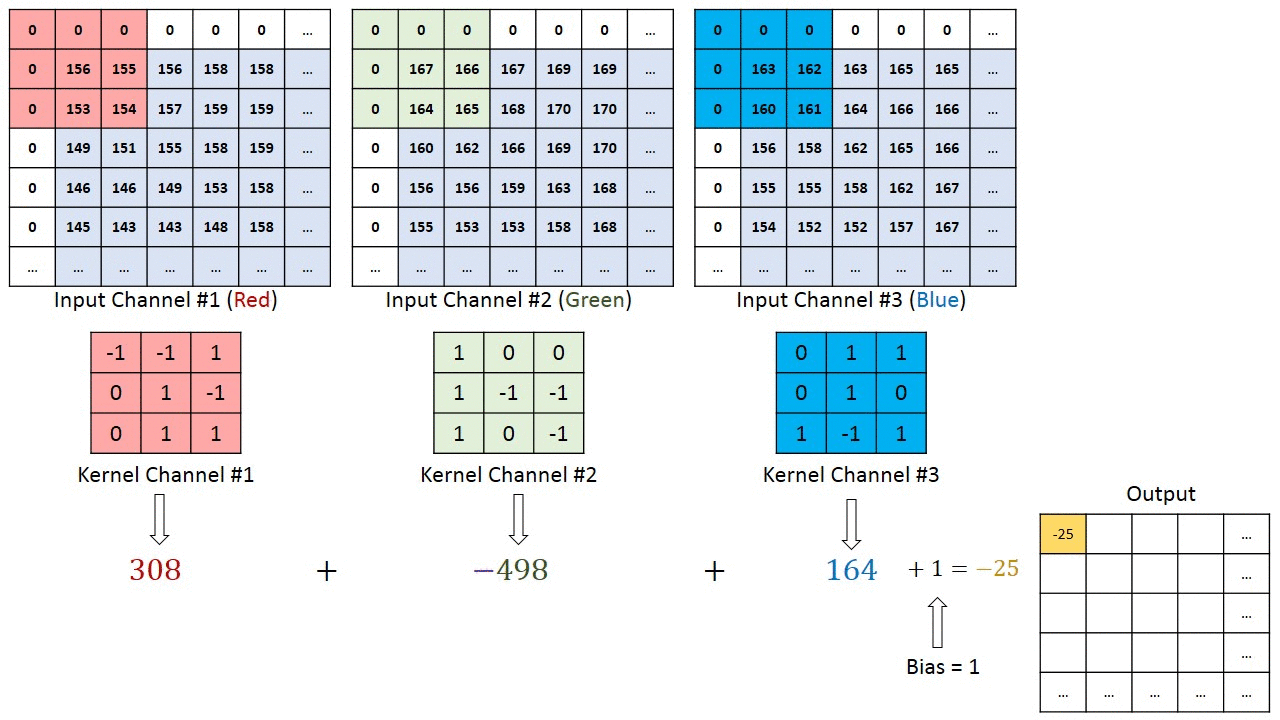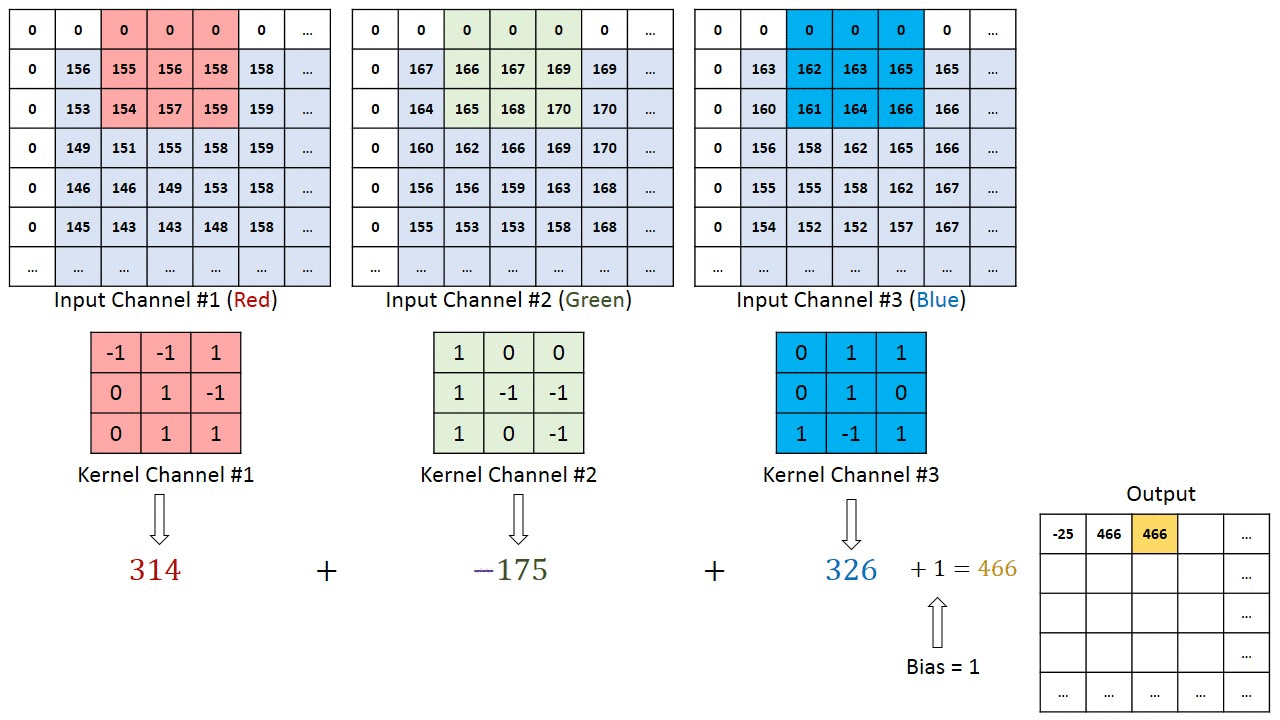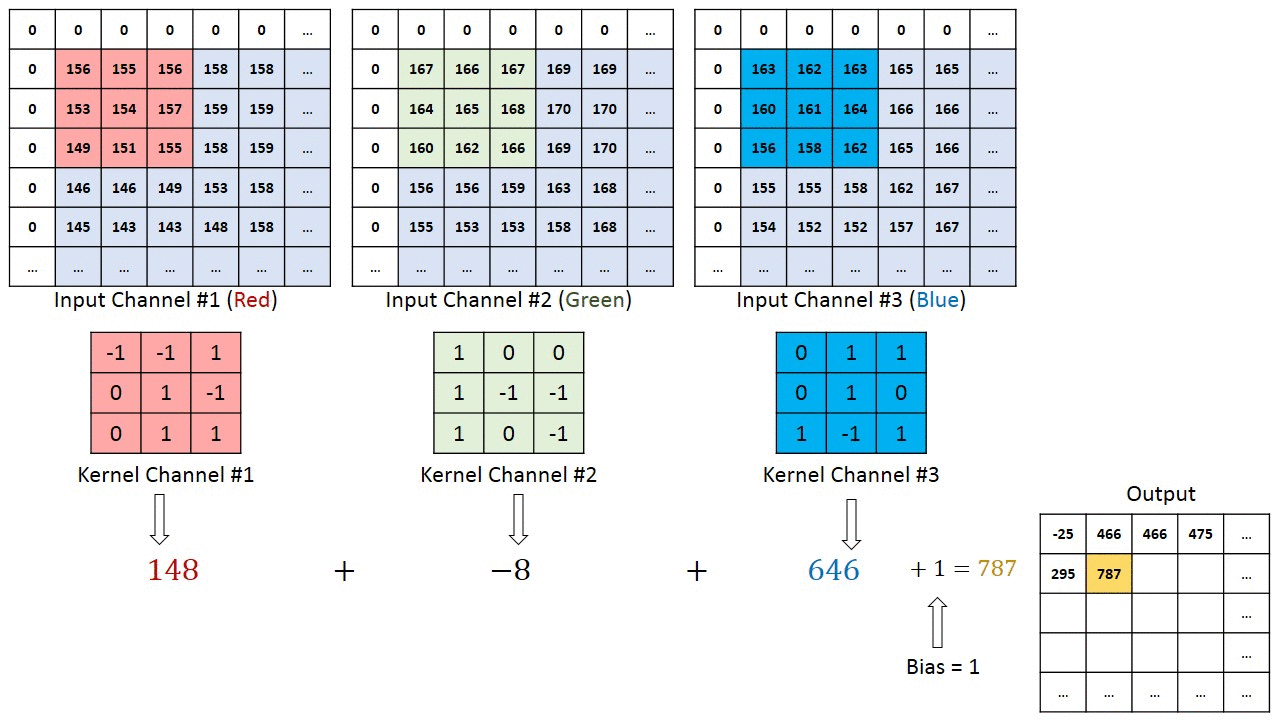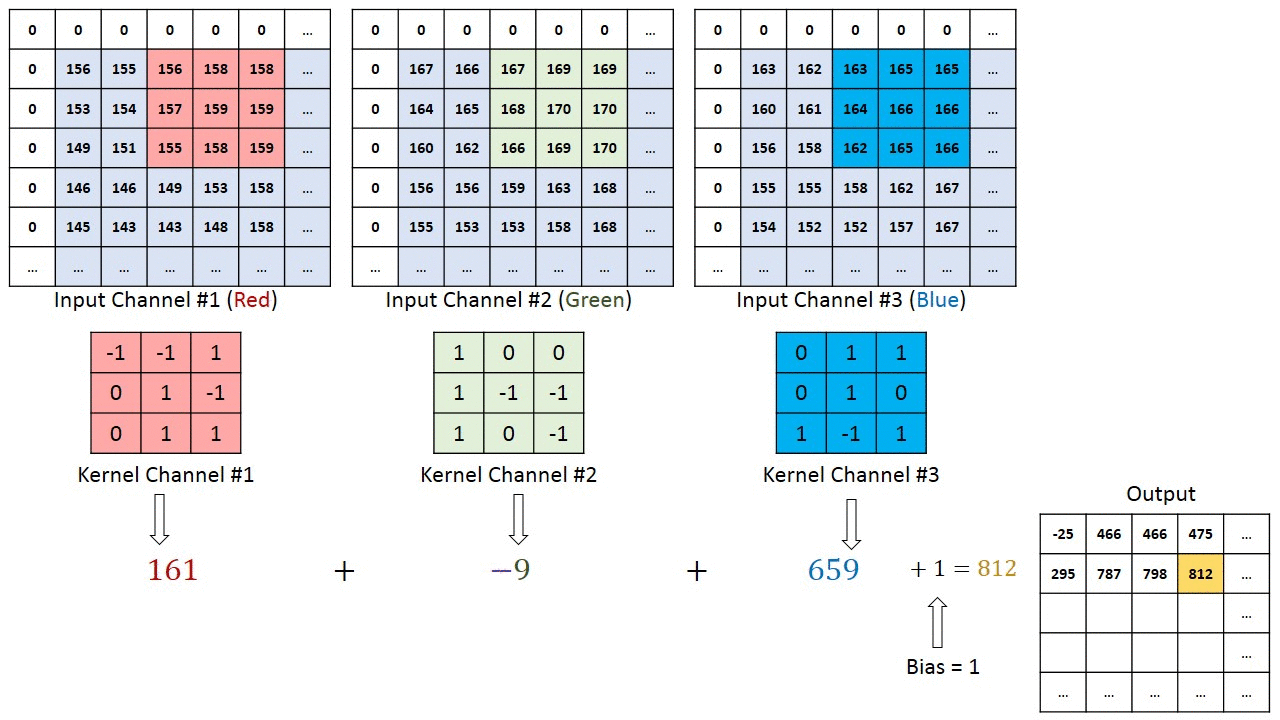 

위 그림은 3x3x3 filter를 이동시키며 output을 얻은 결과이다. 다만 앞의 예제와 다른 점을 발견할 수 있는데, 바로 테두리가 0으로 둘러쌓여 있다는 것이다.

앞의 예제를 다시 보면, 5x5 이미지를 3x3 filter, stride = 1로 했더니 이미지 크기가 3x3으로 줄어들었다. 이렇게 convolution 연산은 이미지 사이즈가 무조건 줄어들게 되어있다. 그런데 이런 현상은 이미지의 정보를 잃게 되는 불이익을 가져다 주기 때문에 주변에 0과 같은 의미없는 값을 넣어 1 pixel씩 키워주면 원래 이미지 사이즈를 유지(same padding)할 수 있다. 이런 기법을 Padding이라 하며, 0으로 테두리를 추가한 경우를 zero padding이라고 한다.

[출처 : https://cs231n.github.io/convolutional-networks]

그리고 Filter를 꼭 하나만 쓰라는 법은 없다. Filter를 여러개 사용한다는 의미는, 이미지에서 여러개의 다른 특징을 찾아내는 것을 의미하며, 당연히 Filter는 복수를 사용해야 한다. 그래야 이미지에서 많은 Feature를 찾아낼 수 있기 때문이다. 위 그림은 3x3x3 Filter를 2개 사용해서 convolution 연산을 하는 예제이다.

2) Sub-sampling (Pooling)

Sub-sampling은 이미지의 topology 변화에 영향을 받지 않게하기 위해 window 내에서 대표값만 기억하는 방법이다. 

[2x2 window, stride=2로 pooling 한 예]

일반적인 sub-sampling은 window의 특정 위치값을 뽑거나 평균값(average pooling)을 사용하는데, 신경망에서는 최대값(max pooling)을 주로 사용한다. 

※ 신경세포학적으로 살펴보면 통상 시신경의 강한 신호만 살아남고 나머지는 무시하기 때문이다. 실제로 우리는 고양이의 전체를 보고 고양이를 인식한다고 생각하지만, 실제 신경세포는 고양이의 강한 특징만 뇌로 전달한다.

[3x3 window, stride=1로 max pooling 하는 모습]

참고로 max pooling도 stride와 padding의 개념을 그대로 적용할 수 있지만, pooling의 목적이 sub-sampling인 만큼 same padding을 적용하는 경우는 잘 없다.

3) Fully Connected Layer

앞에서 설명한 Convolution layer와 Sub-sampling layer를 거치면 local feature를 찾을 수 있다. (직선이나 곡선 등 edge를 찾았을 수 있다)

그리고 그 과정을 반복한다는 것은 local feature에서 또 새로운 feature를 찾는 것을 의미하고, 충분히 반복하다 보면 global feature를 찾게 된다. (직선이나 곡선의 조합으로 고양이의 눈, 귀라는 feature를 찾는 격이다.)

이 단계까지 왔다면 global feature를 학습하는 Fully Connected Layer를 추가할 수 있다. 이제 포스팅 초반에 봤던 이해하기 어려웠던 그림을 다시 한번 살펴보자.

• Conv_1 : (5x5x1) 크기를 갖는 filter(=kernel) n1개를 사용해서 (24x24xn1) 결과를 뽑아냈다. 이미지가 작아진 걸 보니 same padding은 하지 않은 듯 하다.

• Max-Pooling : (2x2) window로 이미지 크기를 절반(12x12)으로 줄였다. stride=2로 max pooling 했기 때문이다.

• Conv_2 : (5x5xn1) 크기를 갖는 filter n2개를 사용해서 (8x8xn2)를 만들어 냈다. 마찬가지로 same padding은 하지 않아 이미지의 크기가 줄었다.

• Max-Pooling : (2x2) window로 다시 한번 이미지 크기를 절반(4x4)로 줄였다.

• Flattened : (4x4)이미지 n2개를 쭉 전개해서 (4x4xn2)개의 노드를 갖는 레이어로 변환했다.

• fc_3 : n3개의 노드를 갖는 fully connected layer를 추가했다. 이때 activation function은 ReLU다.

• fc_4 : 이미지를 classification 하기 위해 class의 갯수인 10개 노드를 가진 FC layer를 추가했다. 이때 출력은 각 class의 확률로 나와야 하기 때문에 softmax가 activation function으로 적용됐을 것이다. 과적합 방지를 위해 dropout 한 것도 확인된다.

하나만 더 살펴보자. 이번에 살펴볼 구조는 Google에서 개발한 아주 유명한 초창기 CNN 모델인 LeNet-5이다.

이제 위와 같은 그림을 보면 어느정도 해석할 수 있어야 한다. 
(참고로 이미지가 흑백으로 보이지만 3개 채널(RGB)을 가진 이미지이다.)

• C1 : (5x5x3) filter 6개를 이용해서 (28x28x6)이미지를 만들었다.
  ※ 파라미터 수 = 5x5x3x6 = 450개

• S2 : (2x2) window, stride=2로 max pooling 해서 이미지 사이즈가 절반으로 줄었다.
  ※ Sub-sampling에는 학습되는 파라미터가 없다. 그냥 연산만 한다.

• C3 : (5x5x6) filter 16개를 이용해서 (10x10x16)이미지를 만들었다.
  ※ 파라미터 수 = 5x5x6x16 = 2,400개

• S4 : (2x2) window, stride=2로 max pooling해서 (5x5x16)이미지를 만들었다.

• C5 : (5x5x16)이미지를 flatten 시키고 120개 노드를 가지는 FC레이어를 추가했다.
  ※ 파라미터 수 = 5x5x16 x 120 = 48,000개

• C6 : 84개 노드를 가지는 FC layer를 추가했다.
  ※ 파라미터 수 = 120 x 84 = 10,080개

• C7 : 10개 노드를 가지는 FC layer를 output layer로 추가했다. (activation = softmax)
  ※ 파라미터 수 = 84 x 10 = 840개

이번에는 레이어를 살펴보면서 필요한 파라미터 수도 세어봤는데 약 61,770개의 파라미터가 필요한 것으로 파악된다. (bias 파라미터 갯수는 세지 않아서 정확하지 않다.)

비록 61,770개가 많아보이지만, 대부분의 파라미터는 FC layer 에서 왔다. (95%) 

즉, CNN은 Convolution을 위한 filter를 학습하기 때문에, 전체 레이어를 FC layer로 구성하는 것보다 월등하게 적은 파라미터를 가진다. 

※ 물론 여전히 학습 파라미터수가 많긴 하고, 그 만큼 학습 데이터도 많이 필요할 것으로 예상된다. (통상 파라미터 갯수 x 10배 데이터가 학습시킨다.) 이 문제 해결을 위해 데이터를 회전, 반전 등을 통해 새로운 데이터를 인위적으로 만드는 기술이 있다. (Data augmentation) 관련해서는 추후에 다시 다루기로 한다.

CNN learns hierarchical representation

앞에서 잠깐 이런 말을 했었다.

• Convolution layer와 Sub-sampling layer를 거치면 local feature를 찾을 수 있다. (직선이나 곡선 등 edge를 찾았을 수 있다)

• 그리고 그 과정을 반복한다는 것은 local feature에서 또 새로운 feature를 찾는 것을 의미하고, 충분히 반복하다 보면 global feature를 찾게 된다. (직선이나 곡선의 조합으로 고양이의 눈, 귀라는 feature를 찾는 격이다.)

정말로 CNN이 Conv + Pooling layer를 거치면서 hierarchical representation을 찾는지 확인해보자.

[출처 : Convolutional deep belief networks for scalable unsupervised learning of hierarchical representation]

위 사례는 각 convolution layer의 channel을 가시화 한 것이다. (embedding 이라 부른다.)

실제로 초기 layer에서는 simple한 특징(ex. 직선, 곡선, 원) 정도의 local feature를 찾아내는데, local feature들로부터 눈, 코, 귀와 같은 특징을 찾아내는 모습을 볼 수 있다. 이렇게 CNN은 계층적(hierarchical)인 특징을 찾으며 학습된다는 것을 알 수 있다.

지금까지 CNN의 원리와 특징, 그리고 CNN Operator들에 대해서 살펴보았다. 이쯤에서 한번 끊고, 다음 글에서 유명한 CNN architecture들을 소개하고, classification의 목적에서 더 나아간 CNN 활용 기법들에 대해 소개하도록 한다.