Logistic Regression
Logistic regression은 분류(Classification)문제를 풀기 위한 가장 기본이 되는 알고리즘이다. 이번 시간에는 Logistic regression을 풀기 위한 Maximum likelihood formulation에 대해 알아보고, 이 함수를 풀기 위한 방법으로 IRLS(Iterative re-weighted least squared)알고리즘에 대해서 알아본다.
※ 본문에서는 Logistic regression의 증명부터 활용까지 다룬다.
대략적인 원리나 개념만 알고 싶은 경우 [데이터마이닝] Logistic Regression을 참고하자.
Binary Classification & Logistic function
분류(Classification)문제는 예측하고자 하는 대상이 continuous real number가 아닌 discrete 한 class인 경우를 말한다. 예를 들면 불량(0) vs. 양품(1) 이라던가, 이미지에서는 개 vs. 고양이 vs. 닭 을 분류하는 문제를 들 수 있다. class의 수가 2개인 경우를 가장 간단한 분류 문제라고 할 수 있는데, Binary classification(이진 분류)에 대해서 알아보도록 하자.
Binary classification의 class가 C1, C2로 주어져 있다.
우리가 구하고자 하는 것은 x라는 feature가 C1일 확률이며, Bayes rule에 의해 아래와 같이 표현될 수 있다.
※ C2일 확률 P(C2 | x)= 1 - P(C1 | x)
※ Bayes rule이 기억 나지 않으면 [AI] Probability 강의노트를 참고하자.
- Bayes rule에 의해 P(C1 | x)를 표현한다.
- P(x)는 각 joint확률 즉, P(x, C1)와 P(x, C2)의 합과 같다.
- 분자로 나눠서 C1과 C2의 비율로 표현되는 식을 만든다.
- 서로 상쇄되는 exp()와 log()를 취한다. 이 때 -log임으로 분자, 분모의 위치가 바뀐다.
- log ratio를 나타내는 항을 ξ로 치환한다.
즉, 우리가 찾고자 하는 모델 P(C1 | x)는 두 사건의 likelihood ratio 와 prior ratio로 표현된 ξ의 함수로 표현 될 수 있으며, 이 함수를 Logistic Function이라 한다.Logistic function은 위와 같이 0과 1사이 값을 갖는 함수인데, 해석해보면 아래의 의미를 갖는다.
- ξ가 크면 즉, C1일 확률이 크면 P(C1 | x)=1로 수렴한다.
- ξ가 작으면 즉, C2일 확률이 크면 P(C1 | x)=0으로 수렴한다.
다음 단계는 P(C1|w, x)를 구할 수 있는 '학습 가능한' 모델을 구현하는 것이다. 즉, weight를 학습할 수 있도록 wTx을 변형시켜줄 필요가 있다. 이 때 위에서 구한 logistic function을 활용하면, 0~1 사이의 확률로 P(C1|w, x)를 구할 수 있다.
실제로 wTx가 크면 1, 작으면 0의 값을 갖도록 할 수 있는데, 만약 y=0인데 wTx가 크다? 그럼 wTx가 작아지도록 w를 튜닝할 수 있다.
Maximum Likelihood Formulation
앞서 위와 같이 Logistic regression 모델을 정의 했다. 이제 남은 것은 weight를 업데이트하기 위한 optimization이다. 그리고 optimization하기 위해서는 현재 모델이 잘 예측하고 있는지를 평가하기 위한 measure가 필요하다. 그 방법에 대해서 알아보자.
먼저 logistic regression은 y가 continuous한 값이 아닌 discrete value로 이루어져 있어서 P(y | x)는 Bernoulli(베르누이) 분포를 따른다.
(부록) Bernoulli 분포 요약
random variable X ∈ {1, 0}로 discrete value를 가지고,
Probability mass function은 위와 같다.
위 식의 x에 0과 1을 대입하면 각각 1-μ와 μ가 나오는 것을 확인할 수 있다.
다시 원래의 문제로 돌아와 Bernoulli 정의를 활용하면 logistic regression의 확률분포를 아래와 같이 표현할 수 있다.
그리고 위 식이 parameter를 가질 수 있게 우리가 정의한 모델 σ(wTx)를 적용하면 아래와 같이 고쳐쓸 수 있다.
※ likelihood는 parameterized distribution 이고, maximum likelihood를 만족하는 parameter를 찾아야하는데 아직은 parameterized 되지 않았다.
이렇게 고치면 parameterized Bernoulli 분포, 즉 likelihood function이 완성된다.
만약에 파라미터가 많다? 아래와 같이 matrix연산으로 치환하고 모두 곱하면 된다.
그리고 계산 편의상 양변에 로그를 취하면 곱이 아니라 합으로 표현된다.
드디어 w를 파라미터로 갖는 log-likelihood function이 완성됐다. 이제 우리가 할 일은 위 식을 최대화 할 수 있는 w를 찾으면 된다.
그런데 위 식을 최대화 하기 위해 미분하는 방법은 적용할 수 없다. 왜냐하면 σ가 비선형 함수라서 closed-form 형태를 띄지 않기 때문에 δL/δw=0 을 찾을 없기 때문이다.
그래서 Iterative하게 즉, w를 조금씩 update 하면서 가장 큰 값을 찾아야 한다. 챕터 1에서 배운 gradient decent가 떠오르지만 최소값이 아닌 최대값을 찾기 때문에 gradient ascent라는 방법으로 찾을 수 있다. (원리는 정확히 똑같다.)
물론 gradient ascent라는 방법을 쓸 수 있지만, 더욱 일반적으로 사용하는 IRLS 알고리즘을 적용시켜보자.
IRLS(Iterative Re-weighted Least Squares)
Gradient / Hessian matrix / Gradient descent & ascent / Newton's method
1. Gradient, Hessian matrix
gradient는 앞서 여러번 다루었기 때문에 간단히 넘어가도록 한다.
함수 f(x)의 gradient는 f(x)를 각 feature의 편미분 값을 갖는 벡터이며, f(x)의 값이 증가하는 방향을 의미한다. 그리고 2-norm을 구하면 벡터의 크기 즉, 기울기가 나온다.
예를 들어 f(x,y) = x2 + y2의 gradient를 구해보면
이므로, (1,1)에서 f값이 최대로 증가하는 방향은 (2,2), 그 기울기는 ∥(2,2)∥= √8 이다.
그런데 두번 미분하면? gradient의 변화량 즉 곡률의 특성을 의미하는 matrix가 나오는데 이 matrix를 Hessian matrix라 한다.
※ 거리 →(미분)→속도→(미분)→가속도(속도의 변화량) by 동역학과 유사하게
함수 →(미분)→Gradient→(미분)→Gradient의 변화량 개념으로 이해하면 조금 더 쉽다.
이 Hessian matrix은 gradient를 미분한 것이기 때문에 gradient가 0인 지점을 찾을 수 있게 해준다. 이 의미를 다시 생각해보면, gradient가 0인 지점은 최소지점 아니면 최대지점이다. 즉, Hessian matrix는 f(x)가 아래로 convex인지 위로 concave한 함수인지를 알려줄 수 있다.
그 구체적인 방법까지는 지금 알 필요는 없지만 간단히 말하면, Hessian matrix의 eigenvalue가 모두 양수(positive-definite)면 아래로 convex하고, 모두 음수면(negative-definite) 위로 convex하다. 모두 섞여 있으면 말의 안장과 같은 saddle point인 의미인데, 관련해서는 추후에 자세히 다루기로 한다.
좀더 쉬운 예를 살펴보면, f(x) = (x-2)2 + 1 함수를 두번 미분하면 f''(x) = 2 > 0 이기 때문에 아래로 convex한 함수임을 알 수 있다.
2. Gradient descent / ascent
3. Newton's method
Newton's method의 기본적인 알고리즘은 이렇다.
만약 우리가 가지고 있는 optimize 함수 J(w)를 2차함수로 근사화할 수 있다면, 그 2차함수의 최소점(w1)으로 파라미터를 update 하는 것이다. 위 그림을 보면 learning rate가 고정된 일반적인 gradient decent보다 획기적으로 빠르게 최소점을 향해 간다. 이 과정을 반복해서 optimize했을 때 통상 gradient decent의 수렴속도의 제곱승만큼 더 빨리 수렴한다고 한다.
이 컨셉이 Newton's method의 핵심인데, 가장 중요한 가정은 J(w)가 convex해야 한다는 것이다. 즉, J(w)의 Hessian matrix가 positive definition을 충족해야지만 적용할 수 있다. (다행인건 logistic regression의 J(w)는 convex하다.)
이제 본격적으로 풀이해보도록 하자.
가장 먼저 optimize 함수 J(w)를 2차 함수로 근사화 해야 한다. 이 때 2nd-order Taylor series expansion 공식을 활용하면 쉽게 근사화 할 수 있다. 이 근사화된 식을 미분하면 아래와 같이 전개된다.
w를 update하는 3번째 줄을 잘 보면 J(w)를 2번 미분한 Hessian과 1번 미분한 Gradient가 보인다. 즉, Newton's method에서는 매 순간의 Hessian inverse matrix가 learning rate역할을 하고 있음을 알 수 있다. 그리고 Hessian matrix가 learning rate에 관여하기 때문에 곡률의 특성을 반영해서 빠르게 weight update가 이루어진다.
4. IRLS
지금까지 Gradient decent / Hessian / Newton's method에 대해서 알아봤는데, 이 원리를 Logistic regression에 적용한 것이 IRLS다.
Logistic regression의 log likelihood function는 위와 같고,
※ 목적함
log likelihood function을 1번 미분해서 Gradient를 구하고,
2번 미분해서 Hessian 을 구한다.
Newton's method는 아래로 convex한 문제에 적용할 수 있기 때문에 minimum log-likelihood 문제로 전환한다. (gradient, Hessian 모두 negative로 변경)
그리고 이것을 Newton's method에 그대로 대입하면 위와 같은 결과가 나온다.
위 식을 조금 예쁘게 표현하기 위해 S와 b를 정의해서 치환하자.
위 식을 가만히 살펴보니 떠오르는 식이 있다.
바로 linear regression에서 Least squared method로 도출한 weight를 구하는 식과 상당히 유사하다. 다만 다른점은 LSM에서는 위 식을 구하면 W가 한번에 계산됐었는데(closed form) 우리가 구한 식은 그렇지 않다.
위 식에서 w가 한번 업데이트 되면 S와 b가 완전히 바뀐다. (y예측값은 w에 dependent하기 때문)
그리고 바뀐 S, b를 활용해서 w를 또 업데이트 한다. 이 행위를 w의 변화가 없을때까지 반복해야 비로서 w를 완성시킬 수 있다.
위와 같이 w가 Iterative하게 Re-weighted 되는데 Least Squares의 형태와 닮았다고 해서 이 방법을 IRLS 알고리즘이라 한다.
Newton's method에서 언급한것과 같이, Newton's method를 응용한 IRLS는 gradient decent에 비해 수렴 속도가 월등히 빠르다. 그래서 대다수의 Logistic regression을 구현한 라이브러리에는 weight의 optimization을 위해 통상 IRLS를 사용하고 있다.
이번에는 w를 업데이트 하고 나면 S, b가 바뀐다. 그래서 다음에도 update되는 양이 달라진다. 그리고 이러 ㄴ현상이 반복되는데, 이렇게 iterative한 특성을 가지고 있으면서 re-weighting이 일어나는 least square와 유사한 알고리즘이라 하여 IRLS라 한다. 가장 standard 알고리즘이다. 대부분 알고리즘은 IRLS로 구현되어 있다. gradient보다 계산량은 많을지라도 converge 하는 속도가 훨씬 빠르다.
아래는 본 글에서 자세히 다루진 않지만 개념이해를 위해 가볍게 숙지하도록 하자.
(부록) link function
모든 분류 회귀모형에는 link function이라는 옵션이 있다. link function은 logit function처럼 선형함수를 0-1 사이의 값을 갖는 함수로 변환해주는 함수이다.
Logistic regression에서는 logit변환을 통해 회귀 모형을 구했다.
하지만 logit변환 외에도 다양한 방법으로 선형함수를 0~1의 값을 갖게 하는 변환 함수들이 있는데, 'regression link function'으로 검색하면 아래와 같이 다양한 함수를 확인할 수 있다. 즉, 선형함수를 0~1로만 변환시킬 수 있다면 logit변환이 아니더라도 얼마든지 분류문제에 확인할 수 있다는 것이다.
- gompit → gomperts function
- probit → 확률누적분포함수
- normit → 정규누적분포함수
여러 변환함수가 있음에도 굳이 logit변환을 사용하는 이유는 해석이 용이하기 때문이다.
(부록) Multi-class logistic regression
y ∈{0, 1, ..., K}면 어떻게 풀까?
이 때 model의 목적은 P(y=1 | x), P(y=2 | x), ... , P(x=k | x)를 모두 구하는 것이다.
x가 주어졌을때 y가 1일 확률, 2일 확률... 즉, k개의 class를 분류하는 모델이 필요하고, 각 사건을 예측하기 위해 x에 곱해질 weight vector가 아래와 같이 k개 필요하다. 이런 문제를 푸는 일반적인 방법은 아래와 같다.
x와 weight의 곱으로 각 사건이 일어날 확률을 구해야하는데 지금은 -∞에서 +∞의 값을 가질 수 있는 상태다. 이것들을 일단 positive한 값을 가질 수 있도록 하자. 가장 쉬운 방법은 지수함수로 만들어 주는 것이다.
이제 각각의 사건을 예측하는 값들이 positive 값을 갖게 되었다. 이것들을 확률로 나타내기 위해 아래와 같이 normalization 할 수 있다.
이제 위 식을 이용하면 x가 주어졌을 때 y=k일 확률을 구할 수 있게 되었다. 즉 Multi-class를 예측하기 위한 softmax regression 모델이 완성됐다.
이렇게 입력받은 값을 0~1사이의 확률로 나타내는 함수를 softmax함수라 한다.
softmax 함수는 이후 Neural Network에서도 자주 등장하니 기억해두도록 하자.
위에서 정의한 softmax regression 모델과 같이 y가 3개 이상의 discrete class를 가질때 y의 분포는 categorical distribution을 가진다. 일종의 Bernoulli distribution의 확장형이다. 그리고 이 때의 probability mass function은 위와 같다.
※ Bernoulli distribution : y ∈ {0, 1} 일 때(binary class) 분포
마지막으로 위 확률분포에 앞서 구한 softmax 함수를 대입하면 아래의 likelihood function을 구할 수 있다.
이제 위 식을 logistic regression때와 같이 IRLS를 적용하면 w를 튜닝할 수 있다.
(부록)Multi-Label Learning
만약 Label이 여러개인 경우는 어떻게 예측할까?
Label이 다수인 것과 Class가 다수인 것은 엄연히 다르다.
Class가 다수라는 것은 Multi-class softmax regression처럼, X를 보고 여러개의 class중 1개일 확률을 계산하는 것이다.
예를 들어 softmax regression은
P(y=개 | x) = 0.8, P(y=고양이 | x) = 0.1, P(y=돼지|x) = 0.1
이렇게 모든 class가 일어날 확률의 합이 1이 되게 예측한다.그래서 y가 특정 class일 확률을 구하기 위해 softmax 함수가 필요하다.
Label이 다수라는 것은 X를 보고 어떤 label의 조건을 만족하는지를 예측하는 것이다.
예를 들어 위 사진을 보고 .
P(y=개 | x) = 0.8, P(y=하늘 | x) = 0.9, P(y=모래|x) = 0.7, P(y=고양이|x) = 0.1
이렇게 여러 label중 1개 label일 확률이 아니라 모든 label이 독립적으로 자체확률을 가진다.
그럼 이런 모델은 어떻게 정의할 수 있을까?
간단하다, logistic regression 모델을 class별로 만들면 된다.
위 말 그대로 각각의 logistic regression을 풀이하면 되기 때문에 자세한 풀이법은 생략한다.

















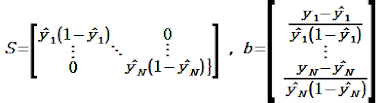



![[빅분기] PART4. 빅데이터 결과 해석 - 분석결과 해석 및 활용 - 분석결과 활용 (출제빈도 : 하)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj2tCMzQ5D2rhqkDfbphh9LKohFnYl3Df8LahM8gskD0BNHA5jX1MLhVIuG78S5IdyrrQrB60ygONq5FvYBLzrUnJrOhKpTfTFzZP0TFS_lZDipN44DhIq8FfFfnieRwTSzDCXvKacFQWvlcETOaoxXS0KNSFdN3apRHi5ReqUer7jCvbIFp2tj8Gmqci3S/w680/%EB%B9%85%EB%8D%B0%EC%9D%B4%ED%84%B0%20%EA%B5%AC%EC%B6%95%EB%B0%A9%EB%B2%95%EB%A1%A0%20%EB%B9%84%EA%B5%90.png)
0 댓글